然后是分治策略的另一个经典例子———二分查找,顾名思义,就是在一个有序(从小到大)的数组中查找一个元素的位置,先从最中间将数组变为两个小数组,然后与中间值进行对比,如果相等直接返回,不相等又分两种情况,如果中间元素比待查找值小,就从后半个数组中继续二分查找,反之,从前半个数组中二分查找。
public static int Binary_Search(int []data, int x, int n){ //data为待搜索数组(有序),x为待搜索元素,n为数组大小 int left = 0, right = n - 1; //指示左右的两个指示器 while(left <= right){ //left可以等于right,因为有可能刚好两个指示器同时指示到了待查找元素上 int mid = (left+right)/2; if(data[mid] > x) right = mid-1; else if(data[mid] < x) left = mid+1; else return mid; } return -1; //表示查找失败 } 棋盘覆盖下面我们逐渐加大难度,接下来这个问题叫做棋盘覆盖,我们先简单介绍一下这个问题。
在一个2^k × 2^k (k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为特殊方格。显然,特殊方格在棋盘中可能出现的位置有4^k种,因而有4^k种不同的棋盘,图4.10(a)所示是k=3时64种棋盘中的一个。棋盘覆盖问题(chess cover problem)要求用图4.10(b)所示的4种不同形状的L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
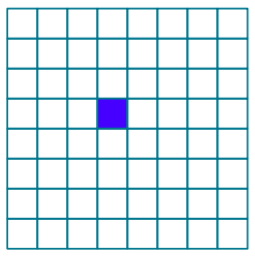
图4.10(a)
图4.10(b)
在这里为了方便讲解,我们采用k=2时候的情况来说明这个问题,设初始情况为
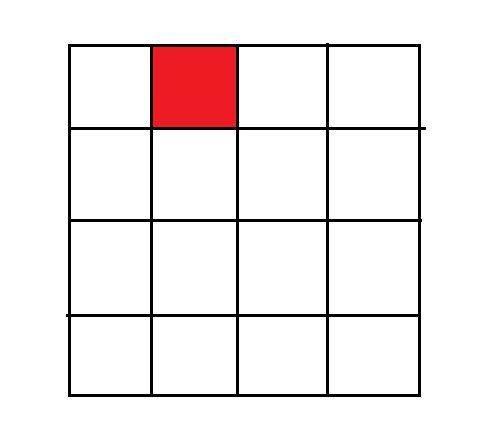
第一次将其分割成四个小块,分成了四个子棋盘,以黄线为分割线
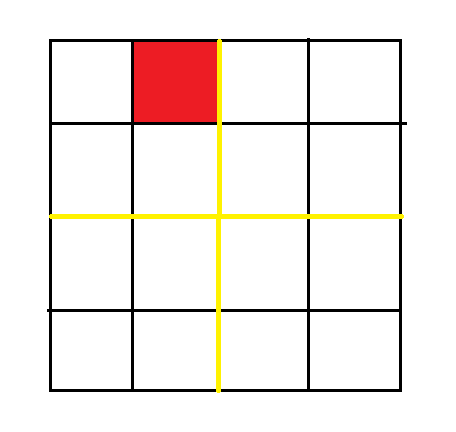
然后分别对其进行填充
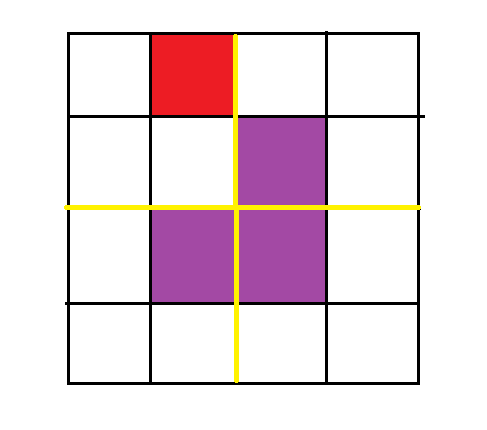
填充完后,又可以将其分割
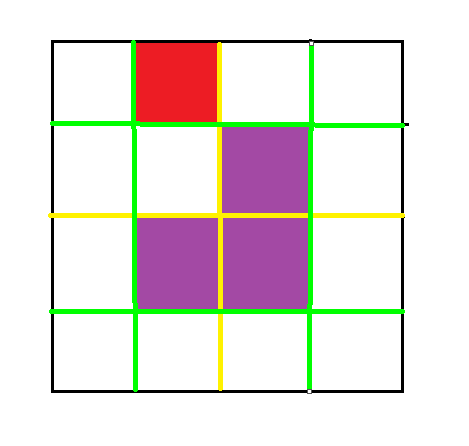
重复上述填充操作,即可对所有方格填充

当k更大的时候的过程可以参考这位大佬的博客棋盘覆盖问题,接下来我们用代码实现。
static int board[][] = new int[4][4]; //棋盘 static int tag = 1; //骨牌编号 /** * 分治算法典例2———棋盘覆盖问题 * @date 2019/11/3 afternoon * @param tr 棋盘左上角方格的行号 * @param tc 棋盘左上角方格的列号 * @param dr 特殊方格所在的行号 * @param dc 特殊方格所在的列号 * @param size 棋盘宽度 * @param s 当前棋盘宽度的一半 * @param tr+s 当前棋盘中间行的行号 * @param tc+s 当前棋盘中间列的列号 */ public static void chess(int tr, int tc, int dr, int dc, int size){ if(size == 1) return; int newtag = tag++; int s = size / 2; //分割棋盘 //覆盖左上角子棋盘 if(dr < tr+s && dc < tc+s){ //特殊方格在此棋盘中 chess(tr,tc,dr,dc,s); }else{ //此棋盘中无特殊方格 board[tr+s-1][tc+s-1] = newtag; chess(tr,tc,tr+s-1,tc+s-1,s); } //覆盖右上角子棋盘 if(dr < tr+s && dc >= tc+s){ chess(tr,tc+s,dr,dc,s); }else{ board[tr+s-1][tc+s] = newtag; chess(tr,tc+s,tr+s-1,tc+s,s); } //覆盖左下角子棋盘 if(dr >= tr+s && dc < tc+s){ chess(tr+s,tc,dr,dc,s); }else{ board[tr+s][tc+s-1] = newtag; chess(tr+s,tc,tr+s,tc+s-1,s); } //覆盖右下角子棋盘 if(dr >= tr+s && dc >= tc+s){ chess(tr+s,tc+s,dr,dc,s); }else{ board[tr+s][tc+s] = newtag; chess(tr+s,tc+s,tr+s,tc+s,s); } }接下来的问题依然有一些难度,叫做打印日程表问题。
日程表问题问题:设有n=2^k个选手参加循环赛,要求设计一个满足以下要求比赛日程表:
1)每个选手必须与其它n-1个选手各赛一次;
2)每个选手一天只能赛一次。
分析,按照上面的要求,可以将比赛表设计成一个n行n-1列的二维表,其中第i行第j列的元素表示和第i个选手在第j天比赛的选手号。

