1、先把 -1 放入栈内。(至于为什么?看到后面你就知道了)
2、、对于遇到的每个 '(' ,我们将它的下标放入栈中。
3、对于遇到的每个 ‘)’ ,我们弹出栈顶的元素并将当前元素的下标与弹出元素下标作差,得出当前有效括号字符串的长度。
通过这种方法,我们继续计算有效子字符串的长度,并最终返回最长有效子字符串的长度。
看不懂?没事,我弄个例子画几个图,例如 s = "( ) ) ( ( ) )",并且用变量 max 来保存最长有效字符串的程度,i 表示当前字符串的下标
0、初始化:max = 0; i = 0。-1 放入栈内
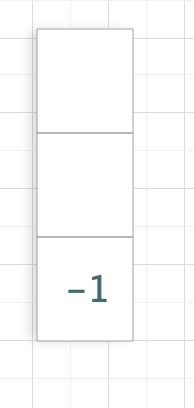
1、i = 0,s[i] = '(',下标 i = 0 入栈

2、i = 1,s[i] = ')',出栈; i - 栈顶元素 = 1 - (-1) = 2,此时 max = 2

3、i = 2,s[i] = ')',出栈;这个时候要注意:由于 -1 出栈后,栈顶没有元素了,所以这个时候我们必须把 ')' 的下标入栈,相当于最开始的初始化。

4、i = 3,s[i] = '(',入栈;
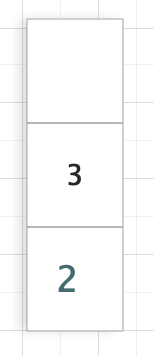
5、i = 4,s[i] = '(',入栈;

6、i = 5,s[i] = ')',出栈;i - 栈顶 = 5 - 3 = 2;此时 max = 2;

7、i = 6,s[i] = ')',出栈;i - 栈顶 = 6 - 2 = 4;此时 max = 4;

8、遍历结束,最长有效括号为 4。
看不大懂?没事,看下代码加深理解勒,代码如下:
public int longestValidParentheses(String s) { int max = 0; Stack<Integer> stack = new Stack<>(); stack.push(-1); for (int i = 0; i < s.length(); i++) { if (s.charAt(i) == '(') { //下标入栈 stack.push(i); } else { // 出栈 stack.pop(); // 看栈顶是否为空,为空的话就不能作差了 if (stack.empty()) { stack.push(i); } else { // i - 栈顶,获得档期有效括号长度 max = Math.max(max, i - stack.peek()); } } } return maxans; }这种做法的时间复杂度为 O(n),空间复杂度为 O(n),能想到用栈来处理,算是很不错的了。
4、最后一击我以为我给出这个解法算是可以的了,面试官应该换一道题的了,然后,面试官又来了一句:还能再优化吗?。这个时候我陷入了沉思.......
看文章的各位大佬们可以想一想在空间上是否还能优化,因为在时间上是不可能优化的了。
想了一会,居然不可以用栈,优化的方案肯定是类似于上面那道题一样,用记录数量的变量来代替栈,然后就被我想出了,具体如下:
实际上,这道题仍然可以像上面那样,用变量来代替栈来优化,不过这个时候我们需要两个变量,我们假设变量为 left 和 right。
我们在从从左到右遍历字符串的过程中,用 left 记录 '(' 的数量,用 right 记录 ')' 的数量。并且在遍历的过程中:
1、如果 left == right,显然这个时候 right 个 ')' 都将一定能够得到匹配。所以当前的有效括号长度为 2 * right。然后更新 max。
2、如果 left < right,显然这个时候部分 ')' 一定得不到匹配,此时我们把 left 和 right 都置为 0。
当遍历完字符串,我们是否就得到最大长度的有效括号了呢?大家可以想一下
答是不可以的,我们还需要从右到左遍历计算一下。
为什么呢?
因为实际上 '(' 和 ')' 其实是等价的,为什么就不可以倒过来遍历计算呢?所以,千万别忽略了哈。

