数据结构与算法之排序 (2)

基本思想：通过一次排序将要排序的数据分割成独立的两个部分，其中一部分的所有数据都比另一部分的所有数据都要小，然后按照这种方法对这两个部分数据分布进行快速排序，整个排序部分可以使用递归进行，以此达到整个数据变成有序序列。

思路分析：

假设数组为arr，左侧为left，右侧为right，设置选择的初始位置为

从左侧开始查找，找到大于等于mid的值为止，从右侧也开始查找，直到找到小于等于mid的值

直到找到l<r的位置，然后递归进行快速排序。

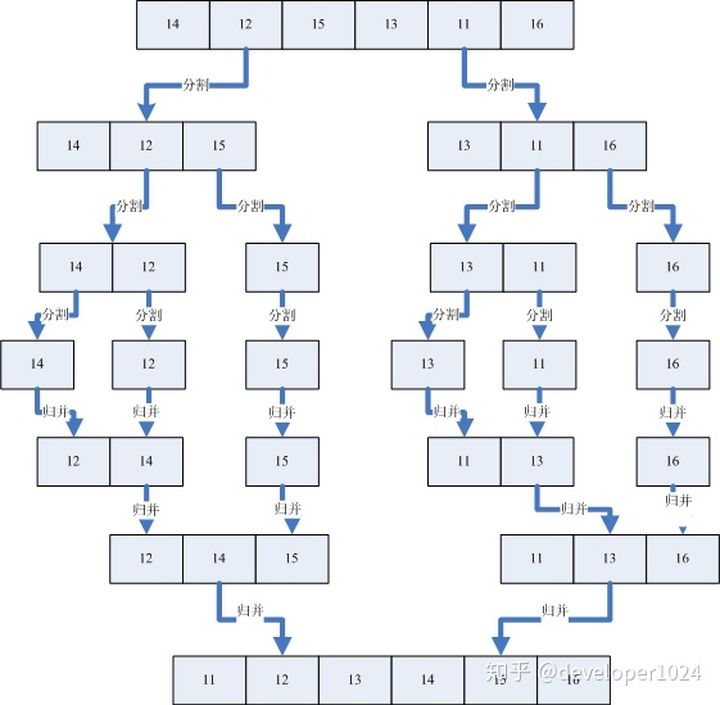
/** * 快速排序 * * @param arr * @param left * @param right * @return */ public static int[] quickSort(int[] arr, int left, int right) { if (left >= right) return null; // 如果数组中left与right相等或者left大于right，则跳出程序 int l = left; int r = right; int mid = arr[(l + r) / 2]; int temp = 0; while (l < r) { while (l < r && arr[l] < mid) { l++; } while (r > l && arr[r] > mid) { r--; } if (l >= r) { break; } temp = arr[l]; arr[l] = arr[r]; arr[r] = temp; if (arr[l] == mid){ r--; } if (arr[r] == mid) { l++; } } quickSort(arr, left, l - 1); quickSort(arr, r + 1, right); return arr; } 5.6 归并排序

归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治策略（分治法将问题分为一些小的问题然后递归求解，而治阶段则将分的阶段得到的各答案“修补”在一起，即分而治之）

基本方法：

首先将数组成分成两个部分，一直拆分直到拆分到每个子数组中只有一个元素

然后进行合并相同相邻的拆分部分，按照顺序进行合并，直到合并成完整的数组

使用递归方法完成最好，时间复杂度为O(nlogn)

/** * 归并排序 * @param arr * @param left * @param right * @return */ public static int[] mergeSort(int[] arr, int left, int right){ // 如果left大于right，说明数组中只有1个或者没有数据，则将直接返回空 if(left >= right) return null; int mid = (left + right)/2; // 分割 mergeSort(arr, left, mid); mergeSort(arr, mid+1, right); int i = left; int j = mid+1; int t = 0; int[] temp = new int[(right - left + 1)]; while (i <= mid && j <= right){ if(arr[i] <= arr[j]){ temp[t] = arr[i]; t ++; i ++; }else { temp[t] = arr[j]; t ++; j ++; } } // 将剩余的内容填充到temp中 while (i <= mid){ temp[t] = arr[i]; t++; i++; } // 将剩余的right内容填充到temp中 while (j <= right){ temp[t] = arr[j]; t++; j++; } // 将temp数据拷贝到arr中 for(int k=left; k<=right; k++){ arr[k] = temp[k-left]; } System.out.println("排序后的数据为：" + Arrays.toString(temp)); return arr; } 5.7 基数排序

基数排序属于“分配式排序”，又称桶子法，它是通过键值的各个位的值，将要排序的元素分配到某些“桶”中，达到排序的作用

基数排序属于稳定性的排序，基数排序法的是效率高的稳定性排序法

基数排序是桶排序的拓展

基数排序的实现方法：将整数位按照位数切割成不同的数字，然后按照每个位分别比较。

实现的方法：

定义一个二维数组，表示10个桶，每一个桶就是一个一维数组

为了防止在放入输的时候数据溢出，则每个一维数组（桶），大小定为arr.length

基数排序就是使用空间换时间的经典算法。

/** * 基数排序 * @param arr * @return */ public static int[] radixSort(int[] arr){ int[][] bubble = new int[10][arr.length]; //设置桶的数量，每个桶最多盛放整个数组 // 寻找数组中最大的数 int max = arr[0]; for(int i=1; i<arr.length; i++){ if(arr[i] > max){ max = arr[i]; } } int maxLength = (max + "").length(); // 根据数值中最大数据的位数判定需要多少次循环 for (int i = 0; i < maxLength; i++) { int[] bubbleLength = new int[10]; // 桶的放的数据的量 // 将数据根据个位、十位、百位依次放入桶中 for (int j = 0; j < arr.length; j++) { int size = arr[j] / (int)Math.pow(10, i) % 10; bubble[size][bubbleLength[size]] = arr[j]; bubbleLength[size] ++; } //依次将数据取出，并放入到原来的数组中 int index = 0; for(int j=0; j<bubble.length; j++){ if(bubbleLength[j] > 0){ for(int k=0; k<bubbleLength[j]; k++){ arr[index++] = bubble[j][k]; } } } } return arr; }