正数n的平方根可以通过计算一系列近似值来获得,每个近似值都比前一个更加接近准确值。第一个近似值是1,接下来的近似值则通过下面的公式来获得。
编写一个程序,读入一个值,计算并打印出它的平方根。如果你将所有的近似值都打印出来,你会发现这种方法获得准确结果的速度有多快。原则上,这种计算可以永远进行下去,它会不断产生更加精确的结果。但在实际中,由于浮点变量的精度限制,程序无法一直计算下去。当某个近似值与前一个近似值相等时,你就可以让程序停止继续计算了。
必须使用浮点变量,而且程序应该对负值输入进行检查。
// 计算一个数的平方根。
#include <stdio.h>
#include <stdlib.h>
int main(){
float new_guess;
float last_guess;
float number;
// 让用户输入,读取数据并对它进行检查。
printf("输入一个数字: " );
scanf("%f", &number );
if( number < 0 ){
printf("无法计算这个数的平方根," "负数! \n");
return EXIT_FAILURE;
}
// 计算平方根的近似值,直到它的值不再变化。
new_guess = 1;
do{
last_guess = new_guess;
new_guess = ( last_guess + number / last_guess ) / 2;
printf ("%.15e\n", new_guess );
} while( new_guess != last_guess );
// 打印结果
printf ("%g 的算术平方根是 %g\n", number, new_guess );
return EXIT_SUCCESS;
}
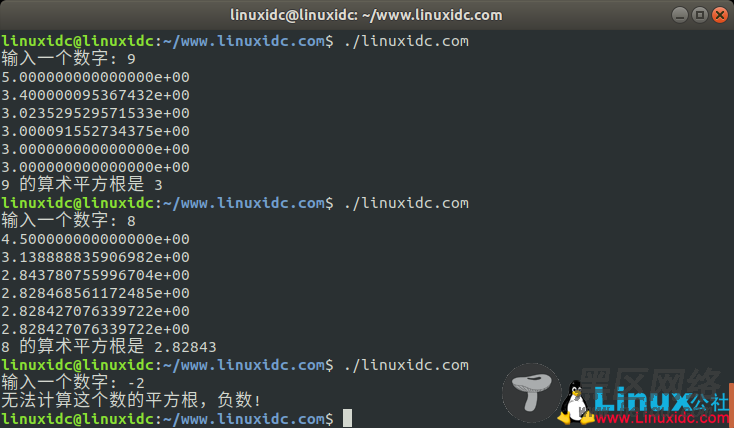
运行结果:
linuxidc@linuxidc:~/www.linuxidc.com$ ./linuxidc.com
输入一个数字: 9
5.000000000000000e+00
3.400000095367432e+00
3.023529529571533e+00
3.000091552734375e+00
3.000000000000000e+00
3.000000000000000e+00
9 的算术平方根是 3
linuxidc@linuxidc:~/www.linuxidc.com$ ./linuxidc.com
输入一个数字: 8
4.500000000000000e+00
3.138888835906982e+00
2.843780755996704e+00
2.828468561172485e+00
2.828427076339722e+00
2.828427076339722e+00
8 的算术平方根是 2.82843
linuxidc@linuxidc:~/www.linuxidc.com$ ./linuxidc.com
输入一个数字: -2
无法计算这个数的平方根,负数!
linuxidc@linuxidc:~/www.linuxidc.com$
Linux公社的RSS地址:https://www.linuxidc.com/rssFeed.aspx

