如上的实现复杂度为N方,可以增加归纳的假设,增加b[k]存储长度为k最长子序列最小结尾元素,那么可以利用二分查找,使用logn查找到插入点,对于每次比较,要么直接比较b【k】比它大直接k+1,更新b【k+1】,要么二分查找到位置,更新b【j】,所以最终复杂度为nlogn(如果数据量大的话,使用该算法较好)

问题5:最长公共子序列长度(LCS)
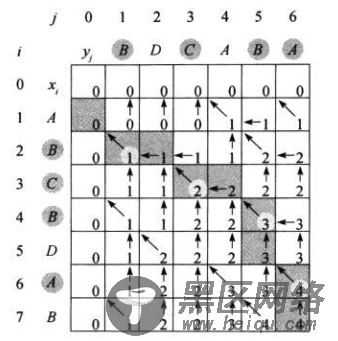
上图可以看出使用了斜侧的比较,所以不能再使用1维数组了
class LCS {
public:
int findLCS(string A, int n, string B, int m) {
if (A.empty()||n==0||B.empty()||m==0)
return 0;
vector<vector<int> > dp(n,vector<int>(m));
//下面是两个for的初始化,当出现第一个相等的时,后面的都直接赋值为1;
for (int i = 0;i < m;i++) {
if (A[0] == B[i]) {
for (int j = i;j < m;j++)
dp[0][j] = 1;
break ;
}
}
for (int i = 0;i < n;i++) {
if (B[0] == A[i]) {
for (int j = i;j < n;j++)
dp[j][0] = 1;
break ;
}
}
for (int i = 1;i < n;i++) {
for (int j = 1;j < m;j++) {
if (A[i] == B[j])
dp[i][j] = dp[i-1][j-1]+1;
else
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[n-1][m-1];
}
};
上面的方法中初始化第一行和第一列有点麻烦,增加了额外的语句,可以增加数组一行和一列来优化代码:
class LCS {
public:
int findLCS(string A, int n, string B, int m) {
vector<vector<int> > dp(n+1,vector<int>(m+1,0));
for (int i =1;i<=n ;++i){
for (int j=1; j<=m; ++j){
if (A[i-1] == B[j-1]){
dp[i][j] = dp[i-1][j-1]+1; //第1行也可以照此直接初始化
}
else {
dp[i][j] = max( dp[i-1][j] ,dp[i][j-1]);
}
}
}
return dp[n][m];
}
};
问题6:背包
N件物品,价值记录在数组V,重量记录在数组W,背包总重量最大为cap,要求总价值最大;

