二叉搜索树是一种特殊的二叉树,它的特点是:
对于任意一个节点p,存储在p的左子树的中的所有节点中的值都小于p中的值
对于任意一个节点p,存储在p的右子树的中的所有节点中的值都大于p中的值
一个图例:
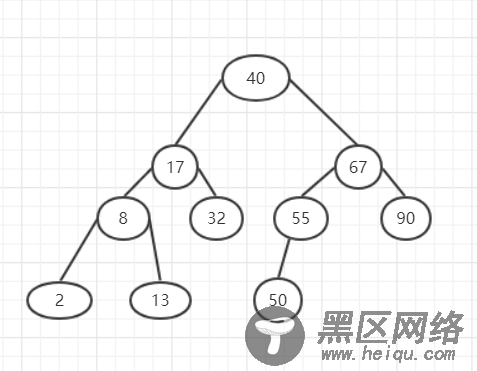
基于二叉搜索树的这种关系,我们可以用它来实现有序映射
遍历二叉搜索树
基于二叉搜索树的特性,采用中序遍历的方式可以使得遍历结果是按照从小到大的顺序排列的。了解中序遍历可以参考用Python实现数据结构之树
这里还需要思考的一个内容是在基于中序遍历的前提下,如何求一个节点的后继节点或前驱节点。
显然这就是求比该节点大的下一个节点或比它小的前一个节点。我们拿求后继节点为例:
当该节点有右孩子时,那么后继结点就是右子树中最左边的节点
当该节点没有右孩子时,那么后继节点就是第一个是左孩子的祖先的父节点
算法用伪代码表示为:
def after(p):
"""寻找二叉搜索树的后继节点的伪代码"""
if right(p) is not None:
walk = right(p)
while left(right(p)) is not None: # 找最左
walk = left(walk)
return walk
else:
walk = p
ancestor = parent(walk)
while ancestor is not None and walk == right(ancestor): # 当walk是左孩子时或walk是根节点时停止
walk = ancestor
ancestor = parent(walk)
return ancestor
找前驱同理
搜索
既然叫做二叉搜索树,那它很重要的一个用途就是搜索,搜索的方式为:
与根节点比较,如果相等则根节点就是要搜索的位置
比根节点小,则递归的与左孩子比较
比根节点大,则递归的与有孩子比较
如果最后没找到,则返回最后一个与之比较的节点,意味着可以在这个节点位置插入刚才搜索的值
算法用伪代码表示为:
def search(T,p,k):
"""二叉树搜索的伪代码,k是要搜索的值"""
if k == p.key():
return p
elif k < p.key() and T.left(p) is not None:
return search(T,T.left(p))
elif k > p.key() and T.right(p) is not None:
return search(T,T.right(p))
return p
搜索的时间与高度有关,是O(h),也就是最坏的情况下为O(n),最好的情况下是O(log(n))
插入
插入算法较简单,它依赖于搜索算法,将搜索的返回的位置的值与key进行比较,
如果相等,则就在此位置修改
如果小于返回位置的值,则插入到返回位置的左孩子
如果小于返回位置的值,则插入到返回位置的右孩子
删除
删除操作较为复杂,因为删除的位置可以是任意的位置,设删除的位置为p
如果删除的位置没有孩子,则直接删了就行
如果删除的位置有一个孩子,则删除之后把它的孩子接到它原来的位置上
如果删除的位置有两个孩子,则:
1.先找到位置p的前驱r,前驱在左子树中
2.把p删除,将r代替p
3.把r原来的位置删除
使用前驱的原因是它必然比p的右子树的所有节点小,也必然比除了r的p的左子树的所有节点大
python实现
我们利用二叉树来实现有序映射
class OrderedMap(BinaryTree,MutableMapping):
"""使用二叉搜索树实现的有序映射"""
class _item():
def __init__(self, key, value):
self.key = key
self.value = value
def __eq__(self, other):
return self.key == other.key
def __ne__(self, other):
return self.key != other.key
def __lt__(self, other):
return self.key < other.key
class Position(BinaryTree.Position):
def key(self):
return self.element().key
def value(self):
return self.element().value
BinaryTree是在之前文章中定义的二叉树类,具体参考用Python实现数据结构之树
首先定义了两个内嵌类,一个表示键值项,一个用于封装节点
然后定义些非公开方法用于其他方法使用:

