这几天看到几篇关于尾递归的文章,之前对尾递归没有多大概念,所以回头研究了一下尾递归。
尾递归的概念
尾递归(Tail Recursion)的概念是递归概念的一个子集。对于普通的递归,由于必须要记住递归的调用堆栈,由此产生的耗用是难以估量的。比如下文中php小节第一个例子使用php写一个阶乘函数,就是由于递归造成了栈溢出的错误。尾递归出现的目的就是消除递归栈耗损这个缺憾的。
从代码层面看,尾递归其实一句话就可以说清楚了:
函数的最后一个操作是递归调用
比如"菲波纳锲"数列的php的递归实现:
复制代码 代码如下:
fibonacci.php
<?php
function fibonacci($n) {
if ($n < 2) {
return $n;
}
return fibonacci($n - 1) + fibonacci($n - 2);
}
var_dump(fibonacci(30));
这是递归函数,但不是尾递归,因为fibonacci的最后一个操作是加法操作。
转化为尾递归:
复制代码 代码如下:
function fibonacci2($n, $acc1, $acc2) {
if ($n == 0) {
return $acc1;
}
return fibonacci2($n-1, $acc2, $acc1 + $acc2);
}
fibonacci2就是一个尾递归,它增加两个累加器acc1和acc2,并给出初始的值。记住:递归转化为尾递归的思想一定是增加累加器,减少递归外操作。
尾递归在不同语言上的应用也是不同的。最常使用的就是函数式编程Erlang,几乎是所有出现递归的函数全部都修改成为尾递归。下面说一下尾递归在几个不同的语言上的表现和应用。
php中的尾递归
我们做个实验
普通递归:
复制代码 代码如下:
<?php
function factorial($n)
{
if($n == 0) {
return 1;
}
return factorial($n-1) * $n;
}
var_dump(factorial(100000000));
尾递归:
复制代码 代码如下:
<?php
function factorial($n, $acc)
{
if($n == 0) {
return $acc;
}
return factorial($n-1, $acc * $n);
}
var_dump(factorial(100000000, 1));
实验结果:
事实证明,
尾递归在php中是没有任何优化效果的!
C中的尾递归
在C中的尾递归优化是gcc编译器做的。在gcc编译的时候加上-O2会对尾递归进行优化
我们可以直接看生成的汇编代码:
(使用gdb, gcc –O2 factorial.c –o factorial; disass factorial)
未加-O2生成的汇编:
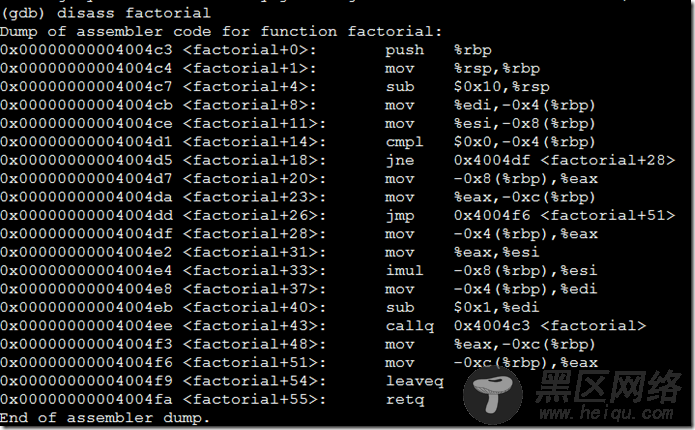
加了O2优化的汇编:
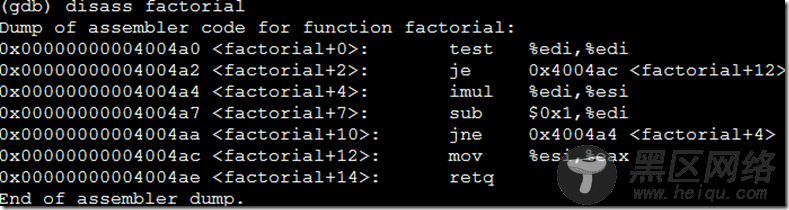
不要头大,我也是初看汇编,但是这份代码非常简单,去网上稍微搜搜命令,大致就能理解:
复制代码 代码如下:
function factoral(n, sum) {
while(n != 0){
sum = n * sum
n = n-1
}
return sum
}
gcc做的确实是智能优化。
如果你还有兴趣,你可以使用-O3对尾递归进行优化,并查看其中的汇编指令
-O3的优化是直接将循环展开
总结
