上一篇文章讨论的二叉搜索树(见 https://www.linuxidc.com/Linux/2019-02/156830.htm),其时间复杂度最好的情况下是O(log(n)),但是最坏的情况是O(n),什么时候是O(n)呢?
像这样:
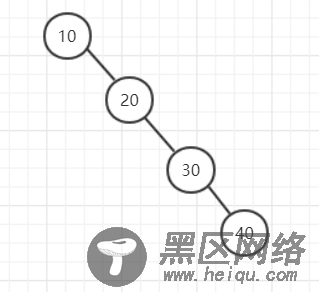
如果先插入10,再插入20,再插入30,再插入40就会成上边这个样子
这个就像是双向链表,我们期望它是下面这个样子:
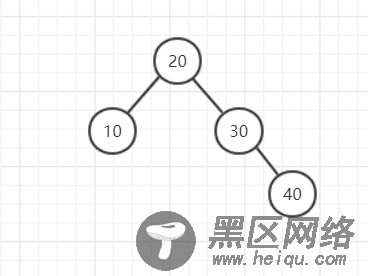
所以我们希望有一种策略能够将第一个图变成第二个图,或者说使树的结构不会产生像第一种图的形式
实现这种策略的一种方式是AVL树
AVL树AVL树的名称是以它的发明家的名字命名的:Adel’son-Vel’skii和Landis
满足高度平衡属性的二叉树就是AVL树
高度平衡属性是:对于树中的每一个位置p,p的孩子的高度最多相差1
很显然前言中的第一个图并不满足高度平衡属性,第二个是满足的。
同时高度平衡属性也意味着一颗AVL树的子树同样是AVL树
并且可以通过证明(这里就不再证了)得到AVL树的高度是O(log n)
所以得出结论,AVL树可以使时间复杂度保持O(log n)
接下来的问题就是怎样保持二叉树的高度平衡属性
保持二叉树的高度平衡属性要保持高度平衡属性的原因是破坏了高度平衡属性
破坏的方式有两种:添加节点与删除节点
添加节点如图:
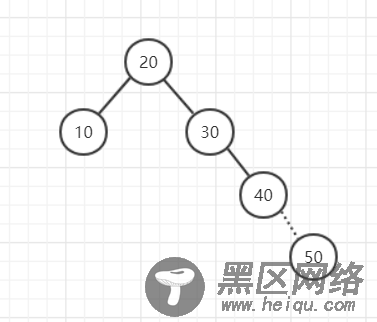
添加50的时候,就会破坏高度平衡属性
删除节点如图:
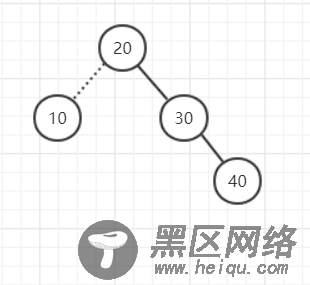
删除10的时候也会破坏高度平衡属性
最后,不论是添加节点还是删除节点,都会使树变成非高度平衡的状态,这种非高度平衡的状态有4种:
1.LL
LL是left-left,可以理解为:首先它不平衡,其次根节点的左子树比右子树高,并且根节点的左子树的左子树比根节点的左子树的右子树高。(从上到下都是左边高)
2.LR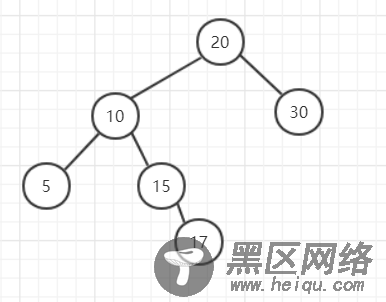
LR是left-right,可以理解为:首先它不平衡,其次根节点的左子树比右子树高,并且根节点的左子树的右子树比根节点的左子树的左子树高。(从上到下先左高后右高)
3.RR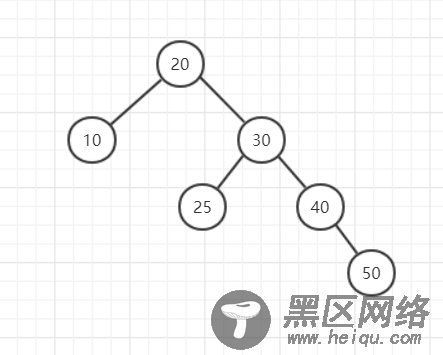
RR是right-right,可以理解为:首先它不平衡,其次根节点的右子树比左子树高,并且根节点的右子树的右子树比根节点的右子树的左子树高。(从上到下都是右边高)
4.RL
RL是right-left,可以理解为:首先它不平衡,其次根节点的右子树比左子树高,并且根节点的右子树的左子树比根节点的右子树的右子树高。(从上到下先右高后左高)
最后,判断是哪种形式的非平衡状态,一定要从不平衡的节点位置看,并不是看4层,比如:
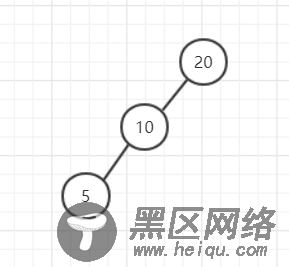
这里只有3层节点,不平衡的节点是20,20的左子树比右子树高,10的左子树比右子树高,所以是LL。(这里的高定义为节点5的高度为1,空节点的高度为0)
接下来是保持高度平衡的调整策略:
同样对于4种不同的形式有4种解决方案:
1.LL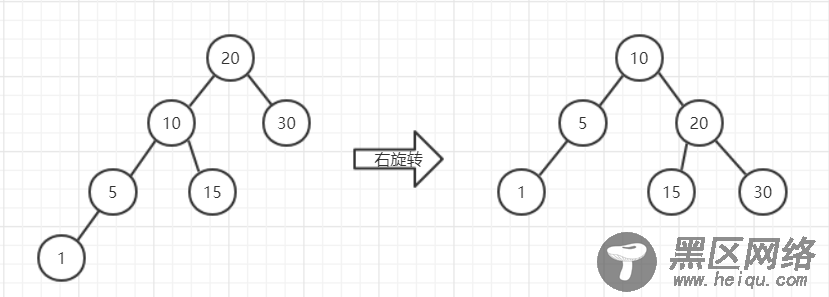
这个变换就像是以10为中心,向右旋转,使10变成根节点,10的左子树不变,右子树变成了20,多余出的15正好挂在由于变换失去了左子树的20的左边。变换后结点从左到右的顺序依然没有变,所以15是正好挂在20的左边的。
2.RR
RR与LL形式差不多,只不顾是反着来的。相当于进行一次左旋转。
RR与LL都只进行一次旋转即可,而LR与RL需要进行两次旋转
3.LR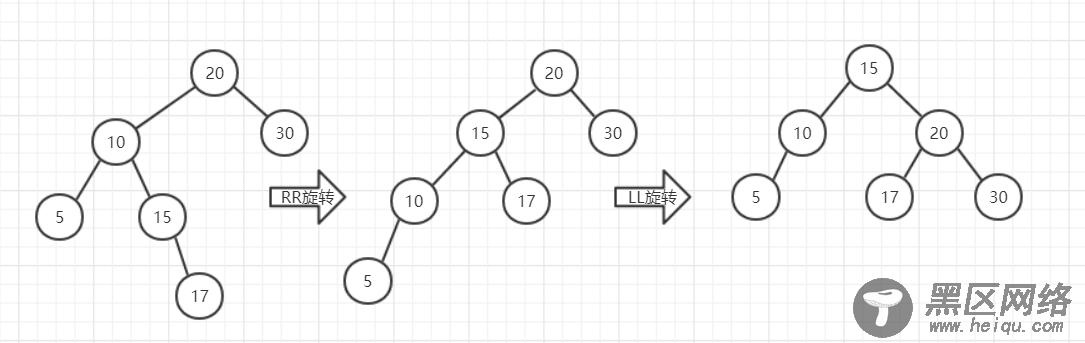
第一次相当于对5、10、15、17这棵子树进行了一次RR旋转,旋转方式与之前的RR方式相同,就像是以15为中心向左旋转,旋转的结果使得整棵树变成了LL的不平衡形态,然后再按照LL的旋转方式对整棵树处理。
4.RL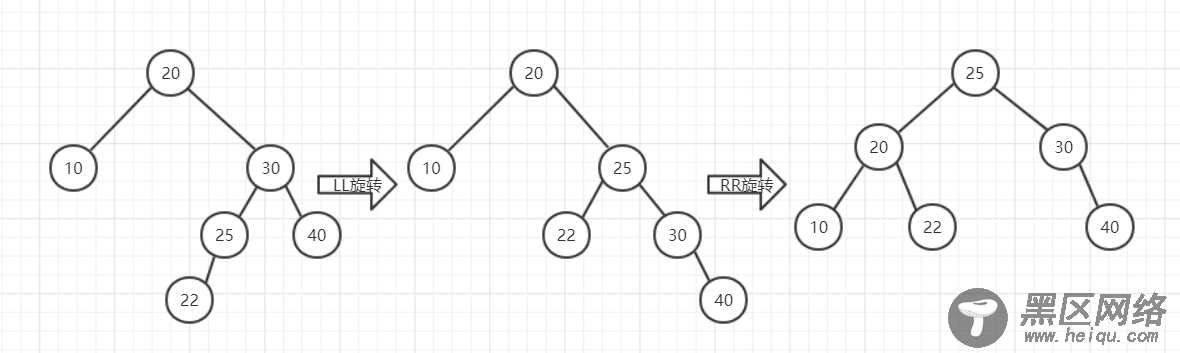
RL同样是LR的相反模式,先将22、25、30、40这棵子树进行LL旋转,再将整棵树进行RR旋转
理解了avl保持平衡从方式后,就可以用代码来实现了
Python实现我们使用AVL对上一篇文章中的有序映射进行优化
因为AVL依赖于节点的高度,所以首先要重写一下Node类:
class AvlTree(OrderedMap):

