二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树:
每个结点都有一个作为搜索依据的关键码(key),所有结点的关键码互不相同。
左子树(如果非空)上所有结点的关键码都小于根结点的关键码。
右子树(如果非空)上所有结点的关键码都大于根结点的关键码。
左子树和右子树也是二叉搜索树。
结点左子树上所有关键码小于结点关键码;
右子树上所有关键码大于结点关键码;
若从根结点到某个叶结点有一条路径,路径左边的结点的关键码不一定小于路径上的结点的关键码。
如果对一棵二叉搜索树进行中序遍历,可以按从小到大的顺序,将各结点关键码排列起来,所以也称二叉搜索树为二叉排序树。 下图为二叉搜索树的一个图
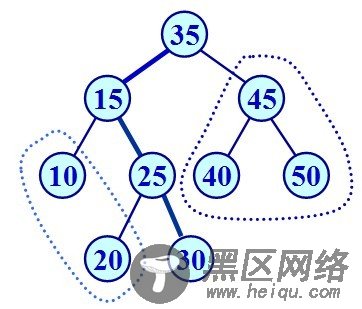
二叉搜索树时一个用于查找操作的搞笑数据结构,因为在最坏的情况下只要查找其中一个分支上的数据就可以了。复杂度为O(nlg n),n为二叉树元素的个数。所以在实际使用中,尽可能的保证二叉树的平衡,这样对搜索来说是最高效的。
二叉树的实现和分析
前面提到,只有当二叉树搜索树保持平衡时对搜索来说才是最高效的,如何保持平衡,实际上很难得。在实际运用中使用最多的就是AVL树,专门在百度百科上专门搜索了下。下面是概述:
********************************************************************************
概述
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。
AVL 节点数计算
高度为 h 的 AVL 树,节点数 N 最多2^h − 1; 最少 (其中)。
最少节点数 n 如以费伯纳西数列可以用数学归纳法证明:
Nh= F【h+ 2】 - 1 (F【h+ 2】是 Fibonacci polynomial 的第h+2个数)。
即:
N0 = 0 (表示 AVL Tree 高度为0的节点总数)
N1 = 1 (表示 AVL Tree 高度为1的节点总数)
N2 = 2 (表示 AVL Tree 高度为2的节点总数)
Nh= N【h− 1】 + N【h− 2】 + 1 (表示 AVL Tree 高度为h的节点总数)
换句话说,当节点数为 N 时,高度 h 最多为。
节点的平衡因子是它的右子树的高度减去它的左子树的高度。带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
操作
AVL树的基本操作一般涉及运做同在不平衡的二叉查找树所运做的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL 旋转"。

