简述一下01背包:
背包容量大小固定,有一些物品,每个物品都有重量和价值两个属性,且物品唯一不重复(即同一物品只能放入一个),放入物品的总重量不能超过背包容量 ,求放入背包的物品的总价值最大化。0代表不放入,1代表放入。
可以通过建表的方式实现01背包,非递归实现。
如果用c[i]表示 i 号物品的重量,v[i]表示 i 号物品的价值,函数f(i,j)表示在有0,1,2...i 号物品和重量限制 j 时能够得到的最大价值,表result[i][j]=f(i,j)
那么可以f(i,j)=max((result[i - 1][j - c[i]] + v[i]),(result[i - 1][j]))查表非递归。
考虑如下:
有一个物品,我们需要考虑该不该把他放入背包中,无非放入和不放入两种情况,那么我们只需要把两种情况下的总价值都算出来,然后取较大的一个就可以了。
result[i - 1][j - c[i]] + v[i]:放入的情况
总价值为 有 i-1 个物品且重量上限为当前上限 j 减去 i 号物品的重量时的价值 result[i - 1][j - c[i]] 加上 i 号物品的价值 v[i]
result[i - 1][j]:不放入的情况,总价值和 i-1 个物品时一样(当前考虑的物品是 i 号物品)
代码部分:
#include<iostream>
#include<string>
using namespace std;
int c[11]; //重量
int v[11]; //价值
int result[11][1001]; //表
///f()函数,计算在i+1个物品和重量上限j的条件下的最大背包价值
int f(int i,int j) //第i个物品,重量上限j //0号物品即第一个物品
{
if (i == 0&&c[i]<=j) //0号物品且重量小于上限
{
return v[i]; //把0号物品放入背包,背包价值为第0号物品的价值
}
if (i == 0 && c[i] > j) //0号物品且重量大于上限
{
return 0; //物品放不进背包,此时背包为空,背包价值为0
}
//不是0号物品的情况
if (i != 0 && j-c[i] >= 0) //i号物品可以放入背包
{
//判断放入和不放入两种情况下背包的价值,选择价值大的方案
return (result[i - 1][j - c[i]] + v[i]) > result[i - 1][j] ? (result[i - 1][j - c[i]] + v[i]) : result[i - 1][j];
} //把这个物品放入背包 //不放入背包
else //i号物品不可以放入背包
return result[i - 1][j];
}
int getResult(int top, int num)
{
if (num == 0) //有0个物品
return 0;
else
{
for (int i = 0; i < num; i++) //第i个物品
{
for (int j = 0; j <= top; j++) //重量
{
result[i][j] = f(i,j); //建表,result[i][j]表示有0,1,2...i个物品和j的重量限制下的最大背包价值
}
}
return result[num-1][top];
}
}
int main()
{
int top; //背包容量
int num; //物品数量
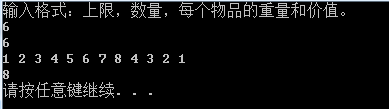
cout << "输入格式:上限,数量,每个物品的重量和价值。" << endl;
cin >> top;
cin >> num;
for (int i = 0; i < num; i++) //第i个物品的重量和价值
{
cin >> c[i] >> v[i];
}
cout << getResult(top, num) << endl;
return 0;
}
测试样例1:

测试样例2:

测试样例3: