4 HTTPS 原理介绍 4.1 内容加密
加密算法一般分为两种,对称加密和非对称加密。所谓对称加密(也叫密钥加密)就是指加密和解密使用的是相同的密钥。而非对称加密(也叫公钥加密)就是指加密和解密使用了不同的密钥。

图 2 对称加密

图 3 非对称加密
对称内容加密强度非常高,一般破解不了。但存在一个很大的问题就是无法安全地生成和保管密钥。假如客户端软件和服务器之间每次会话都使用固定的,相同的密钥加密和解密,肯定存在很大的安全隐患。如果有人从客户端端获取到了对称密钥,整个内容就不存在安全性了,而且管理海量的客户端密钥也是一件很复杂的事情。
非对称加密主要用于密钥交换(也叫密钥协商),能够很好地解决这个问题。浏览器和服务器每次新建会话时都使用非对称密钥交换算法协商出对称密钥,使用这些对称密钥完成应用数据的加解密和验证,整个会话过程中的密钥只在内存中生成和保存,而且每个会话的对称密钥都不相同(除非会话复用),中间者无法窃取。
非对称密钥交换很安全,但同时也是 HTTPS 性能和速度严重降低的“罪魁祸首”。想要知道 HTTPS 为什么影响速度,为什么消耗资源,就一定要理解非对称密钥交换的整个过程。
下面重点介绍一下非对称密钥交换的数学原理及在 TLS 握手过程中的应用。
4.1.1 非对称密钥交换在非对称密钥交换算法出现以前,对称加密一个很大的问题就是不知道如何安全生成和保管密钥。非对称密钥交换过程主要就是为了解决这个问题,使得对称密钥的生成和使用更加安全。
密钥交换算法本身非常复杂,密钥交换过程涉及到随机数生成,模指数运算,空白补齐,加密,签名等操作。
常见的密钥交换算法有 RSA,ECDHE,DH,DHE 等算法。它们的特性如下:
RSA:算法实现简单,诞生于 1977 年,历史悠久,经过了长时间的破解测试,安全性高。缺点就是需要比较大的素数(目前常用的是 2048 位)来保证安全强度,很消耗 CPU 运算资源。RSA 是目前唯一一个既能用于密钥交换又能用于证书签名的算法。
DH:diffie-hellman 密钥交换算法,诞生时间比较早(1977 年),但是 1999 年才公开。缺点是比较消耗 CPU 性能。
ECDHE:使用椭圆曲线(ECC)的 DH 算法,优点是能用较小的素数(256 位)实现 RSA 相同的安全等级。缺点是算法实现复杂,用于密钥交换的历史不长,没有经过长时间的安全攻击测试。
ECDH:不支持 PFS,安全性低,同时无法实现 false start。
DHE:不支持 ECC。非常消耗 CPU 资源。
建议优先支持 RSA 和 ECDH_RSA 密钥交换算法。原因是:
1, ECDHE 支持 ECC 加速,计算速度更快。支持 PFS,更加安全。支持 false start,用户访问速度更快。
2, 目前还有至少 20% 以上的客户端不支持 ECDHE,我们推荐使用 RSA 而不是 DH 或者 DHE,因为 DH 系列算法非常消耗 CPU(相当于要做两次 RSA 计算)。
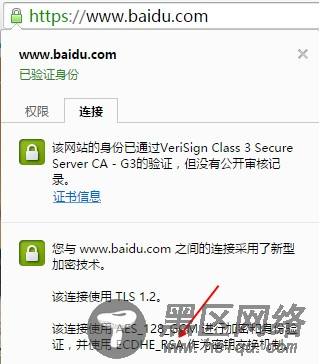
需要注意通常所说的 ECDHE 密钥交换默认都是指 ECDHE_RSA,使用 ECDHE 生成 DH 算法所需的公私钥,然后使用 RSA 算法进行签名最后再计算得出对称密钥。
非对称加密相比对称加密更加安全,但也存在两个明显缺点:
1, CPU 计算资源消耗非常大。一次完全 TLS 握手,密钥交换时的非对称解密计算量占整个握手过程的 90% 以上。而对称加密的计算量只相当于非对称加密的 0.1%,如果应用层数据也使用非对称加解密,性能开销太大,无法承受。
2, 非对称加密算法对加密内容的长度有限制,不能超过公钥长度。比如现在常用的公钥长度是 2048 位,意味着待加密内容不能超过 256 个字节。
所以公钥加密目前只能用来作密钥交换或者内容签名,不适合用来做应用层传输内容的加解密。
非对称密钥交换算法是整个 HTTPS 得以安全的基石,充分理解非对称密钥交换算法是理解 HTTPS 协议和功能的关键。
下面分别通俗地介绍一下 RSA 和 ECDHE 在密钥交换过程中的应用。
4.1.1.1 RSA 密钥协商 4.1.1.1.1 RSA 算法介绍RSA 算法的安全性是建立在乘法不可逆或者大数因子很难分解的基础上。RSA 的推导和实现涉及到了欧拉函数和费马定理及模反元素的概念,有兴趣的读者可以自行百度。
RSA 算法是统治世界的最重要算法之一,而且从目前来看,RSA 也是 HTTPS 体系中最重要的算法,没有之一。
RSA 的计算步骤如下:
1, 随机挑选两个质数 p, q,假设 p = 13, q = 19。 n = p * q = 13 * 19 = 247;
2, ∅(n) 表示与整数 n 互质数的个数。如果 n 等于两个质数的积,则∅(n)=(p-1)(q-1) 挑选一个数 e,满足 1< e <∅(n) 并且 e 与互质,假设 e = 17;
3, 计算 e 关于 n 的模反元素, ed=1 mod ∅(n) , 由 e = 17 ,∅(n) =216 可得 d = 89;
4, 求出了 e,和 d,假设明文 m = 135,密文用 c 表示。那么加解密计算如下:

实际应用中,(n,e) 组成了公钥对,(n,d)组成了私钥对,其中 n 和 d 都是一个接近 22048的大数。即使现在性能很强的 CPU,想要计算 m≡c^d mod(n),也需要消耗比较大的计算资源和时间。
公钥对 (n, e) 一般都注册到了证书里,任何人都能直接查看,比如百度证书的公钥对如下图,其中最末 6 个数字(010001)换算成 10 进制就是 65537,也就是公钥对中的 e。e 取值比较小的好处有两个:
1, 由 c=m^e mod(n) 可知,e 较小,客户端 CPU 计算消耗的资源较少。
2, 加大 server 端的破解难度。e 比较小,私钥对中的 d 必然会非常大。所以 d 的取值空间也就非常大,增加了破解难度。
那为什么 (n,e) 能做为公钥公开,甚至大家都能直接从证书中查看到,这样安全吗?分析如下:
由于 ed≡1 mod ∅(n),知道了 e 和 n,想要求出私钥 d,就必须知道∅(n)。而∅(n)=(p-1)*(q-1),必须计算出 p 和 q 才能确定私钥 d。但是当 n 大到一定程度时(比如接近 2^2048),即使现在最快的 CPU 也无法进行这个因式分解,即无法知道 n 是由哪个数 p 和 q 乘出来的。所以就算知道了公钥,整个加解密过程还是非常安全的。
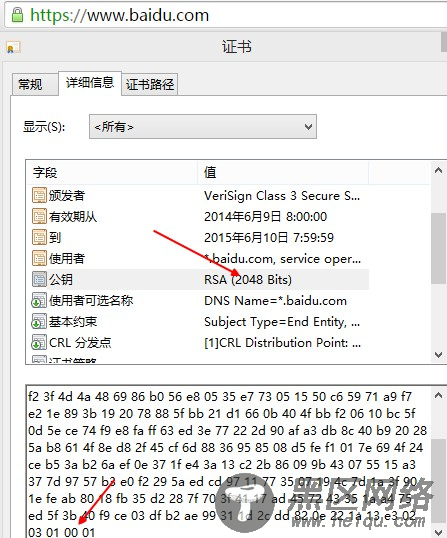
图 5 百度 HTTPS 证书公钥
4.1.1.1.2 握手过程中的 RSA 密钥协商介绍完了 RSA 的原理,那最终会话所需要的对称密钥是如何生成的呢?跟 RSA 有什么关系?
以 TLS1.2 为例简单描述一下,省略跟密钥交换无关的握手消息。过程如下:
1, 浏览器发送 client_hello,包含一个随机数 random1。
2, 服务端回复 server_hello,包含一个随机数 random2,同时回复 certificate,携带了证书公钥 P。
3, 浏览器接收到 random2 之后就能够生成 premaster_secrect 以及 master_secrect。其中 premaster_secret 长度为 48 个字节,前 2 个字节是协议版本号,剩下的 46 个字节填充一个随机数。结构如下:
Struct{byteVersion[2];bute random[46];}
master secrect 的生成算法简述如下:
Master_key= PRF(premaster_secret,“master secrect”, 随机数1+随机数2)
其中 PRF 是一个随机函数,定义如下:
PRF(secret, label, seed)= P_MD5(S1, label + seed) XOR P_SHA-1(S2, label + seed)
从上式可以看出,把 premaster_key 赋值给 secret,”master key”赋值给 label,浏览器和服务器端的两个随机数做种子就能确定地求出一个 48 位长的随机数。
而 master secrect 包含了六部分内容,分别是用于校验内容一致性的密钥,用于对称内容加解密的密钥,以及初始化向量(用于 CBC 模式),客户端和服务端各一份。
至此,浏览器侧的密钥已经完成协商。
4, 浏览器使用证书公钥 P 将 premaster_secrect 加密后发送给服务器。
5, 服务端使用私钥解密得到 premaster_secrect。又由于服务端之前就收到了随机数 1,所以服务端根据相同的生成算法,在相同的输入参数下,求出了相同的 master secrect。
RSA 密钥协商握手过程图示如下:

图 6 RSA 密钥协商过程
可以看出,密钥协商过程需要 2 个 RTT,这也是 HTTPS 慢的一个重要原因。而 RSA 发挥的关键作用就是对 premaster_secrect 进行了加密和解密。中间者不可能破解 RSA 算法,也就不可能知道 premaster_secrect,从而保证了密钥协商过程的安全性。
4.1.1.2 ECDHE 密钥协商
4.1.1.2.1 DH 与 ECC 算法原理ECDHE 算法实现要复杂很多,主要分为两部分:diffie-hellman 算法(简称为 DH)及 ECC(椭圆曲线算术)。他们的安全性都是建立在离散对数计算很困难的基础上。
简单介绍一下 dh 算法的实现,先介绍两个基本概念:
本原根:如果整数 a 是素数 p 的本原根,则 a, a^2, …, a^(p-1) 在 mod p 下都不相同。
离散对数:对任意整数 b 和素数 p 的本原根 a,存在唯一的指数 i 满足:
b ≡ a^i mod p (0≤i≤p-1)
则称 i 是 b 的以 a 为底的模 p 的离散对数。
理解这两个概念,dh 算法就非常简单了,示例如下:
假设 client 和 server 需要协商密钥,p=2579,则本原根 a = 2。
1, Client 选择随机数 Kc = 123 做为自己的私钥,计算 Yc = a^Kc mod p = 2^123 mod 2579 = 2400,把 Yc 作为公钥发送给 server。
2, Server 选择随机数 Ks = 293 作为私钥,计算 Ys = a^Ks mod p = s^293 mod 2579 = 968,把 Ys 作为公钥发送给 client。
3, Client 计算共享密钥:secrect = Ys^Kc mod (p) = 968^123 mod(2579) = 434
4, Server 计算共享密钥:secrect = Yc^Ks mod(p) =2400^293 mod(2579) =434
上述公式中的 Ys,Yc,P, a, 都是公开信息,可以被中间者查看,只有 Ks,Kc 作为私钥没有公开,当私钥较小时,通过穷举攻击能够计算出共享密钥,但是当私钥非常大时,穷举攻击肯定是不可行的。
DH 算法有一个比较大的缺陷就是需要提供足够大的私钥来保证安全性,所以比较消耗 CPU 计算资源。ECC 椭圆曲线算术能够很好的解决这个问题,224 位的密钥长度就能达到 RSA2048 位的安全强度。
ECC 的曲线公式描述的其实不是椭圆,只是跟椭圆曲线周长公式形似才叫椭圆曲线加密算术。ECC 涉及到了有限域、群等近世代数的多个概念,就不做详细介绍了。
ECC 安全性依赖于这样一个事实:
P = kQ, 已知 k, Q 求出 P 相对简单,但是已知 P 和 Q 求出 k 却非常困难。
上式看起来非常简单,但有如下约束条件:
1, Q 是一个非常大的质数,p, k, q 都是椭圆曲线有限域上的离散点。
2, 有限域定义了自己的加法和乘法法则,即使 kQ 的运算也非常复杂。
ECC 应用于 Diffie-Hellman 密钥交换过程如下:
1, 定义一个满足椭圆方程的有限域,即挑选 p, a, b 满足如下方程:
y^2 mod p =(x^3+ax +b) mod p
2, 挑选基点 G = (x, y),G 的阶为 n。n 为满足 nG = 0 的最小正整数。
3, Client 选择私钥 Kc (0 <Kc<n ),产生公钥 Yc =Kc *G
4, server 选择私钥 Ks 并产生公钥 Ys =Ks*G
5, client 计算共享密钥 K = Kc*Ys ,server 端计算共享密钥 Ks*Yc ,这两者的结果是一样的,因为:
Kc*Ys=Kc*(Ks*G)=Ks*(Kc*G)=Ks*Yc
由上面描述可知,只要确定 p, a, b 就能确定一条有限域上的椭圆曲线,由于不是所有的椭圆曲线都能够用于加密,所以 p, a, b 的选取非常讲究,直接关系曲线的安全性和计算速度。
Openssl 实现的,也是 FIPS 推荐的 256 位素数域上的椭圆曲线参数定义如下:
质数 p =115792089210356248762697446949407573530086143415290314195533631308867097853951
阶 n =115792089210356248762697446949407573529996955224135760342422259061068512044369SEED= c49d3608 86e704936a6678e1139d26b7819f7e90c=7efba1662985be9403cb055c75d4f7e0 ce8d84a9 c5114abcaf317768 0104fa0d
椭圆曲线的系数 a =0
椭圆曲线的系统 b =5ac635d8 aa3a93e7 b3ebbd55 769886bc651d06b0 cc53b0f63bce3c3e 27d2604b
基点 G x =6b17d1f2 e12c4247 f8bce6e5 63a440f277037d812deb33a0f4a13945 d898c296
基点 G y =4fe342e2 fe1a7f9b 8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5
简单介绍了 ECC 和 DH 算法的数学原理,我们看下 ECDHE 在 TLS 握手过程中的应用。
相比 RSA,ECDHE 需要多发送一个 server_key_exchange 的握手消息才能完成密钥协商。
同样以 TLS1.2 为例,简单描述一下过程:
1, 浏览器发送 client_hello,包含一个随机数 random1,同时需要有 2 个扩展:
a) Elliptic_curves:客户端支持的曲线类型和有限域参数。现在使用最多的是 256 位的素数域,参数定义如上节所述。
b) Ec_point_formats:支持的曲线点格式,默认都是 uncompressed。
2, 服务端回复 server_hello,包含一个随机数 random2 及 ECC 扩展。
3, 服务端回复 certificate,携带了证书公钥。
4, 服务端生成 ECDH 临时公钥,同时回复 server_key_exchange,包含三部分重要内容:
a) ECC 相关的参数。
b) ECDH 临时公钥。
c) ECC 参数和公钥生成的签名值,用于客户端校验。
5, 浏览器接收 server_key_exchange 之后,使用证书公钥进行签名解密和校验,获取服务器端的 ECDH 临时公钥,生成会话所需要的共享密钥。
至此,浏览器端完成了密钥协商。
6, 浏览器生成 ECDH 临时公钥和 client_key_exchange 消息,跟 RSA 密钥协商不同的是,这个消息不需要加密了。
7, 服务器处理 client_key_exchang 消息,获取客户端 ECDH 临时公钥。
8, 服务器生成会话所需要的共享密钥。
9, Server 端密钥协商过程结束。
图示如下:
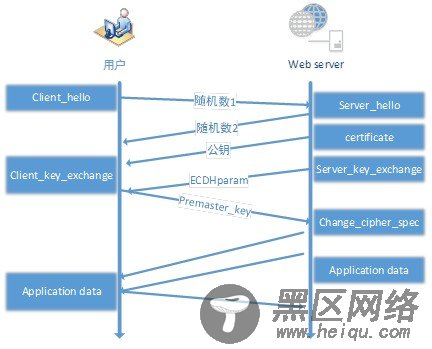
图 7 ECDHE 密钥协商过程
4.1.2 对称内容加密非对称密钥交换过程结束之后就得出了本次会话需要使用的对称密钥。对称加密又分为两种模式:流式加密和分组加密。流式加密现在常用的就是 RC4,不过 RC4 已经不再安全,微软也建议网站尽量不要使用 RC4 流式加密。
一种新的替代 RC4 的流式加密算法叫 ChaCha20,它是 google 推出的速度更快,更安全的加密算法。目前已经被 Android 和 chrome 采用,也编译进了 google 的开源 openssl 分支 —boring ssl,并且。
分组加密以前常用的模式是 AES-CBC,但是 CBC 已经被证明容易遭受BEAST和LUCKY13 攻击。目前建议使用的分组加密模式是 AES-GCM,不过它的缺点是计算量大,性能和电量消耗都比较高,不适用于移动电话和平板电脑。


