向堆中添加一个元素,在堆的内部要进行一个上浮的操作,保证用数组实现的二叉堆还符合我们最大堆的性质(父节点的值大于两个子节点的值)。
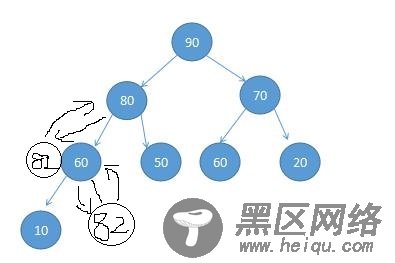
82大于他的父节点60,两个结点交换位置,82还大于他的父结点80,两个节点交换位置。80小于现在的父结点90,结束交换。这个操作很多人称为上浮操作(个人认为名称贴切)上浮操作完成。
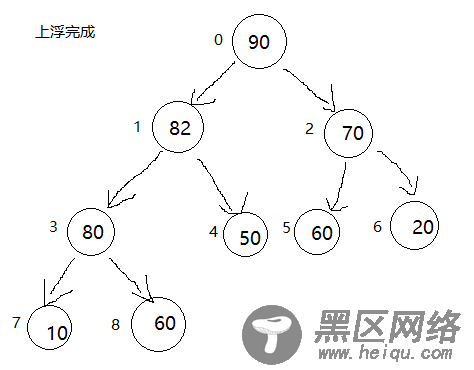
用代码实现我们刚才的操作,已经知道他父结点的位置(公式),交换两个人的位置就变得很简单,MaxHeap添加函数。
//堆中添加元素
public void add(E e)
{
data.addLast(e);
siftUp(data.getSize() - 1);
}
//上浮操作
private void siftUp(int i)
{
while (i > 0 && data.get(parent(i)).compareTo(data.get(i)) < 0)
{
//交换位置
data.swap(i,parent(i));
i = parent(i)
}
}
Array类,添加交换位置的函数
public void swap(int i,int j) { if (i < 0 || i >= size || j < 0 || j > size) { throw new IllegalArgumentException("索引越界"); } E t = data[i]; data[i] = data[j]; data[j] = t; }
有添加就有取出,取出堆中元素其实很简单,因为最大堆决定了只取堆顶元素(数组的第一个元素),直接取出即可。困难的是如何维护二叉堆的性质不变。
取出堆顶元素后
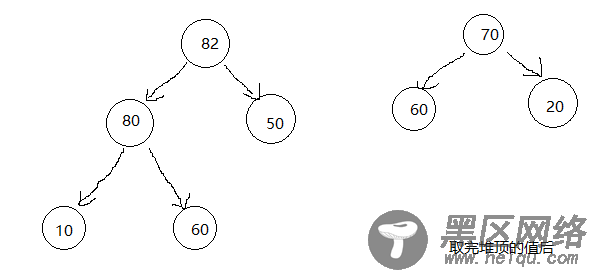
取出堆顶元素,剩下两个子树,将两颗子树糅合成一个二叉堆,现在直接将60这个元素作为堆顶,就满足了完全二叉树的性质但并不符合最大堆性质。

和上浮的操作相反,现在我们要进行下沉的操作,60的左右孩子都比60来得大,要选择左右孩子最大的那个数进行交换,82和60进行交换,80比60来得大,交换他们的位置,10比60来得小,符合二叉堆的性质。交换结束。
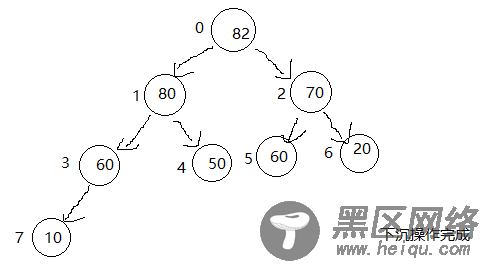
用代码描述刚才取出的操作。
MaxHeap类
//堆中最大元素 public E findMax() { if (data.getSize() == 0) { throw new IllegalArgumentException("堆为空,无法查看值"); } return data.get(0); } //取出堆顶元素 public E extractMax() { E ret = findMax(); data.swap(0,data.getSize() - 1); data.removeLast(); siftDown(0); return ret; } //下沉操作 private void siftDown(int i) { //比较到他左右孩子那个比他大进行交换操作 while (leftChild(i) < data.getSize()) { int j = leftChild(i); if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) //右节点 { j = rightChild(i); } if (data.get(i).compareTo(data.get(j)) >= 0) { break; } data.swap(i,j); i = j; } }
现在我们堆结构基本完成,简单测试一下
Main类

