题目描述:有3扇关闭的门,一扇门后面停着汽车,其余门后是山羊,只有主持人知道每扇门后面是什么。参赛者可以选择一扇门,在开启它之前,主持人会开启另外一扇门,露出门后的山羊,然后允许参赛者更换自己的选择。
1、按照你的第一感觉回答,你觉得不换选择能有更高的几率获得汽车,还是换选择能有更高的几率获得汽车?或几率没有发生变化?
答:更换选择能有更高的几率获得汽车(强烈的求生欲)
2、请自己认真分析一下“不换选择能有更高的几率获得汽车,还是换选择能有更高的几率获得汽车?或几率没有发生变化?” 写出你分析的思路和结果。
答:若参赛者佛系选门,选中车的概率为1/3,选中羊的概率为2/3。如果参赛者选中的是羊并且更换选择,那么他一定会得到车,选中车且更换选择就一定会得到羊,所以在更换的情况下,藏有羊的概率2/3就是他最终获得车的概率,藏有车的概率1/3就是他最终获得羊的概率。如果参赛者打死也不换,那么藏有车的概率1/3就是他获得车的概率,藏有羊的概率2/3就是他获得羊的概率。
3、请设法编写程序验证自己的想法,验证的结果支持了你的分析结果,还是没有支持你的分析结果,请写出程序运行结果,以及其是否支持你的分析。(提示:可以借助随机数函数完成此程序)
答:某一次运行结果:
更换则胜利的次数1998528,失败的次数1001472,胜利百分比66.6176%
不更换则胜利的次数1001472,失败的次数1998528,胜利百分比33.382400000000004%
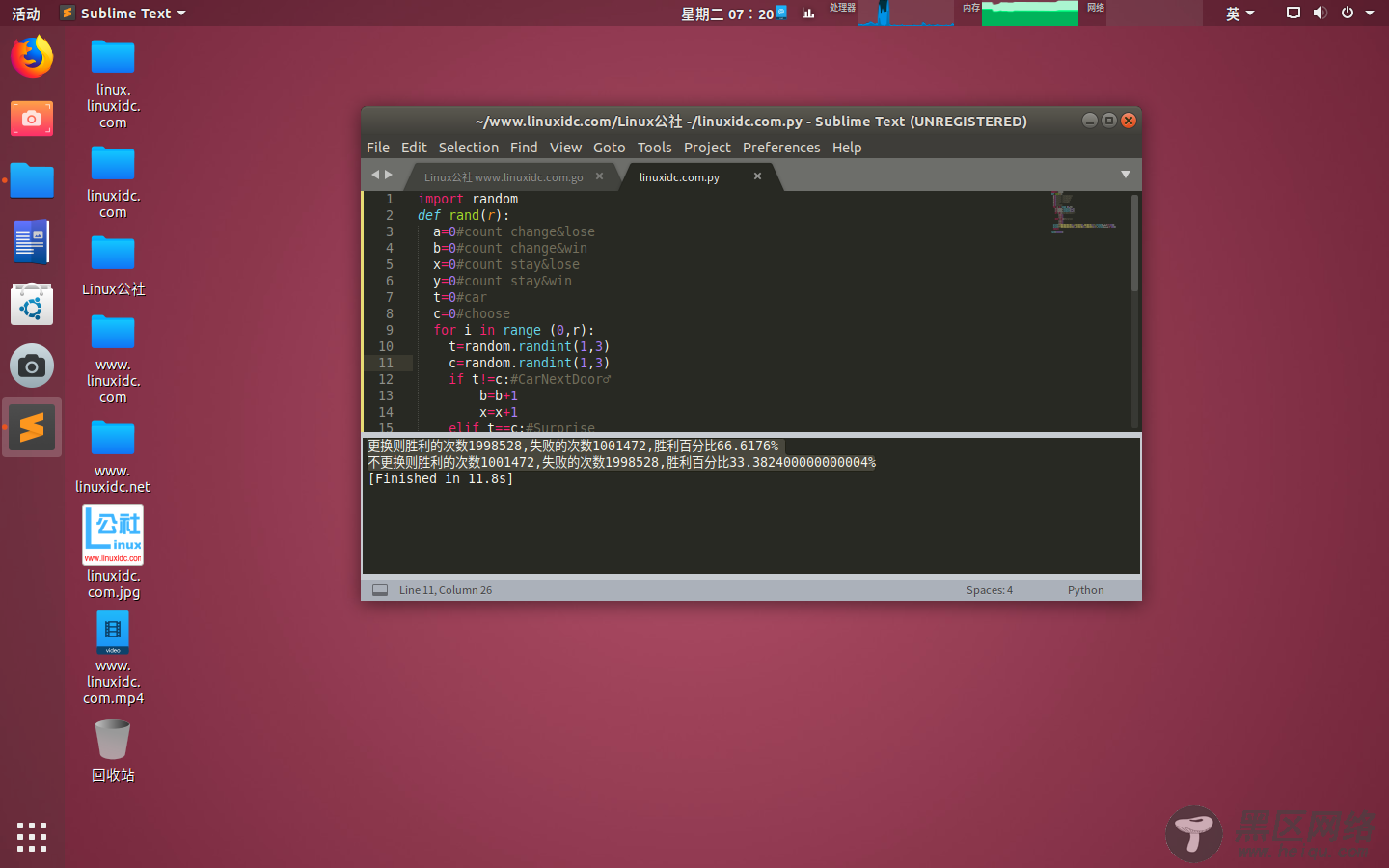
和理论值很接近了(有点慢=_=)。
4、请附上你的代码。(提示:使用编辑器中的插入代码功能,将代码显示为 Python 风格)
代码如下:
import random
def rand(r):
a=0#count change&lose
b=0#count change&win
x=0#count stay&lose
y=0#count stay&win
t=0#car
c=0#choose
for i in range (0,r):
t=random.randint(1,3)
c=random.randint(1,3)
if t!=c:#CarNextDoor♂
b=b+1
x=x+1
elif t==c:#Surprise
a=a+1
y=y+1
print('更换则胜利的次数{},失败的次数{},胜利百分比{}%'.format(b,a,b/r*100))
print('不更换则胜利的次数{},失败的次数{},胜利百分比{}%'.format(y,x,y/r*100))
return

