归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之),将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序,若将两个有序表合并成一个有序表,称为二路归并
1、归并排序的基本思想
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列
2、归并排序的算法描述
第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针超出序列尾,将另一序列剩下的所有元素直接复制到合并序列尾
归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分(递归实现)
(2)“合并”——将划分后的序列段两两合并后排序
如何合并?
在每次合并过程中,都是对两个有序的序列段进行合并,然后排序。
这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。
先将他们合并到一个局部的暂存数组R2中,带合并完成后再将R2复制回R中。
我们称 R[low, mid] 第一段,R[mid+1, high] 为第二段。
每次从两个段中取出一个记录进行关键字的比较,将较小者放入R2中,最后将各段中余下的部分直接复制到R2中。
经过这样的过程,R2已经是一个有序的序列,再将其复制回R中,一次合并排序就完成了。
3、代码实现
/* 将序列对半拆分直到序列长度为1*/
void MergeSort_UptoDown(int *num, int start, int end)
{
int mid = start + (end - start) / 2;
if (start >= end)
{
return;
}
MergeSort_UptoDown(num, start, mid);
MergeSort_UptoDown(num, mid + 1, end);
Merge(num, start, mid, end);
}
void Merge(int *num, int start, int mid, int end)
{
int *temp = (int *)malloc((end-start+1) * sizeof(int)); //申请空间来存放两个有序区归并后的临时区域
int i = start;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= end)
{
if (num[i] <= num[j])
{
temp[k++] = num[i++];
}
else
{
temp[k++] = num[j++];
}
}
while (i <= mid)
{
temp[k++] = num[i++];
}
while (j <= end)
{
temp[k++] = num[j++];
}
//将临时区域中排序后的元素,整合到原数组中
for (i = 0; i < k; i++)
{
num[start + i] = temp[i];
}
free(temp);
}
4、拆分过程
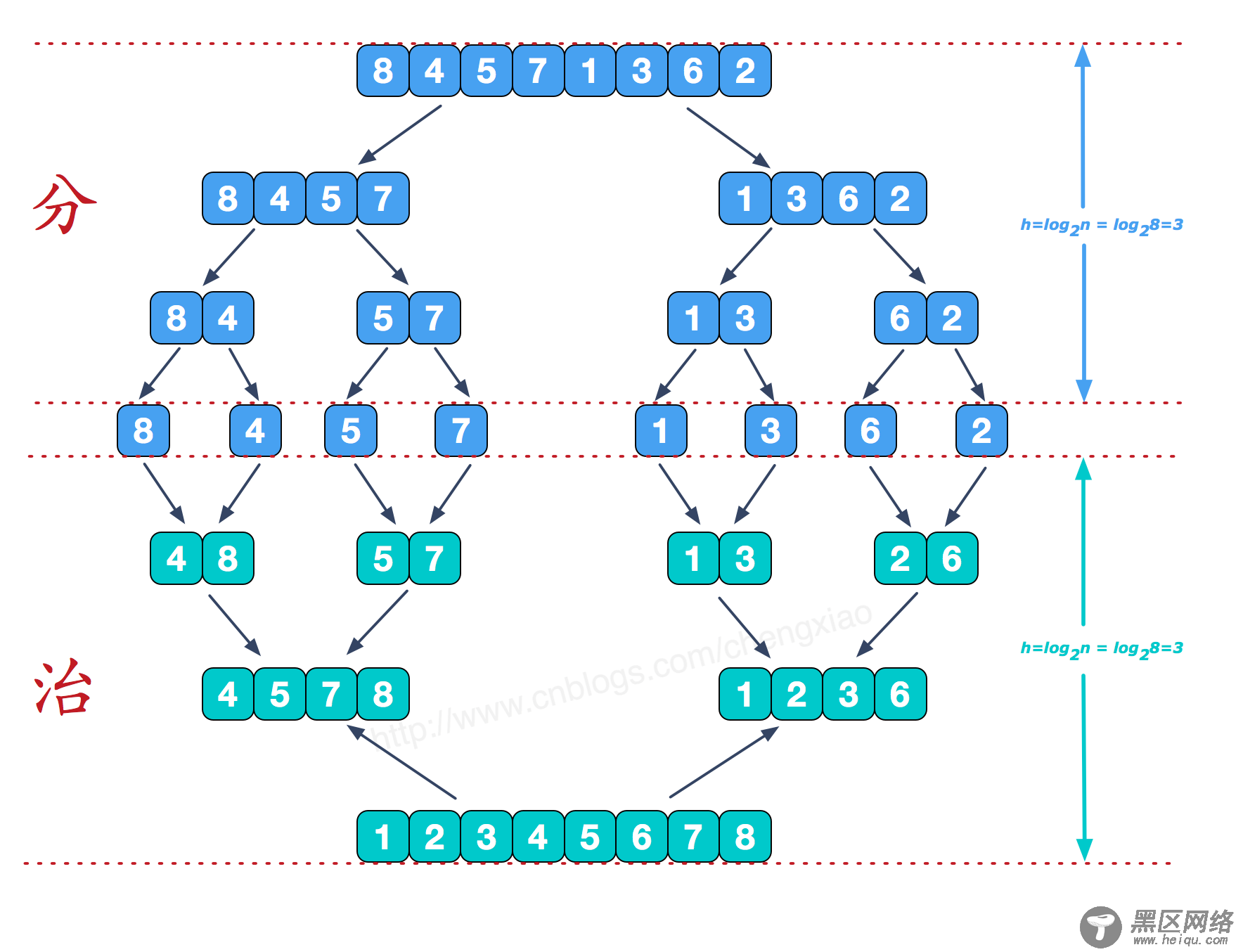
(图片来源:https://www.cnblogs.com/chengxiao/p/6194356.html)
完整代码:
#include <stdio.h>
#include <stdlib.h>
void MergeSort_UptoDown(int *num, int start, int end);
void Merge(int *num, int start, int mid, int end);
int main()
{
/* 归并排序(升序) */
int num[10] = {5, 1, 8, 4, 7, 2, 3, 9, 0, 6};
int length = sizeof(num) / sizeof(num[0]);
int i;
MergeSort_UptoDown(num, 0, length - 1);
for (i = 0; i < length; i++)
{
printf("%d ", num[i]);
}
return 0;
}
/* 将序列对半拆分直到序列长度为1*/
void MergeSort_UptoDown(int *num, int start, int end)
{
int mid = start + (end - start) / 2;
if (start >= end)
{
return;
}
MergeSort_UptoDown(num, start, mid);
MergeSort_UptoDown(num, mid + 1, end);
Merge(num, start, mid, end);
}

