void postorder(BiTree T)
{
BiTree pre,cur;
LinkStack s;
InitStack(&s);
cur = pre = T;
Push(&s,cur);
while(!EmptyStack(s))
{
GetTop(s,&cur); //当前结点的左右孩子都为空,pre为cur的左孩子或者右孩子时,出栈并输出当前结点
if((cur->lchild == NULL && cur->rchild == NULL) || cur->lchild == pre || cur->rchild == pre)
{
Pop(&s,&cur);
printf("%c ",cur->data);
pre = cur; //更新当前结点
}
else
{
if(cur->rchild) //否则入栈右孩子,左孩子
{
Push(&s,cur->rchild);
}
if(cur->lchild)
{
Push(&s,cur->lchild);
}
}
}
}
第五种遍历算法:
此种非递归遍历算法思想可以像递归遍历一样通过修改部分的顺序做到:前中后序三种遍历。
不过便利往往带来的是代码结构上的复杂,此种算法所借助的栈和上面的遍历算法借助的栈不同。
上面的算法使用的栈存储的数据时一个二叉树结点指针,而此算法栈储存的是一个结构体
栈数据类型定义:
typedef struct { // 栈数据定义 BiTree ptr; int task; }Datatype;
其中,task有两个值,0表示访问,1表示遍历。所有结点的task的初始值为1
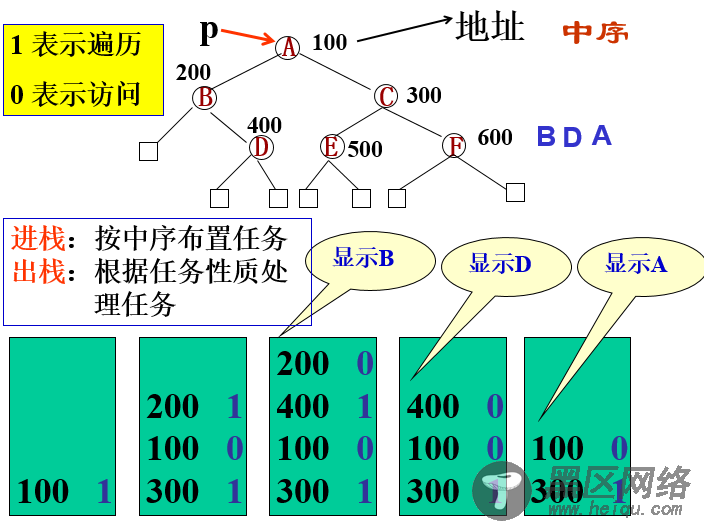
算法思路:
1.根结点先进栈,task初始化为1
2.出栈,若当前结点的task为0 则访问当前结点,task为1,则修改task为0,并按想要的遍历顺序入栈左右孩子结点。
例如:若中序遍历,则先入栈右孩子结点,当前结点,左孩子结点。(其他遍历顺序则改一下入栈顺序)
3.直到栈空,停止循环
此算法完整代码:
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
typedef struct binode{ //二叉树结点定义
char data;
struct binode * lchild,*rchild;
}BiNode,*BiTree;
//非递归遍历所要用到的栈
#define MAX 50
typedef struct { // 栈数据定义
BiTree ptr;
int task;
}Datatype;
typedef struct {
Datatype * arr;
int top;
int stacksize;
}SqStack;//顺序栈
void InitStack(SqStack *S) //初始化字符栈
{
S->arr = (Datatype*)malloc(sizeof(Datatype)*MAX);
if(S->arr == NULL)
{
printf("初始化失败....\n");
exit(0);
}
S->top = -1;
S->stacksize = MAX;
}
int Push(SqStack *S,Datatype ch)//进栈(字符栈)
{
Datatype *p;
int select;
if(S->top+1 == S->stacksize) //先判断栈是否已满
{
printf("栈的容量已满,无法进栈");
return 0;
}
S->arr[++S->top] = ch;
return 1;
}

