如此循环,右边无序区只剩一个元素,则排序完成!
#include<iostream> using namespace std; void sort(int k[],int n) { int min,temp; //min用来保存最小的元素的下标 for(int i = 0;i < n-1; i++) { min = i; for(int j = i+1; j < n; j++) //找出无序区中的最小的元素 { if(k[j] < k[min]) min = j; } if(min != i) //如果最小的元素,不是初始的,即有比它更小的就交换位置 { temp = k[min]; k[min] = k[i]; k[i] = temp; } } } int main() { int k[10] = {2,5,4,6,3,8,9,7,1,0}; sort(k,10); for(int i = 0;i < 10;i++) cout<<k[i]<<" "; } 堆排序堆排序采用大顶堆或着小顶堆,我们这里采用大顶堆来排序。
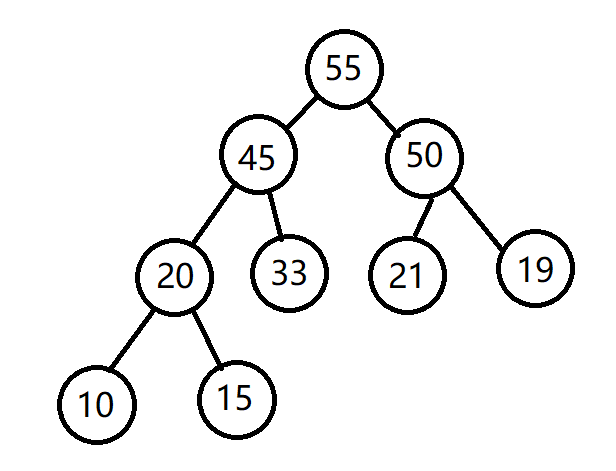
用一棵完全二叉树来模拟一个大顶堆,大顶堆的规则如下:每个结点的值都大于它的孩子结点的值,如下图:
这样,如果我们每次将大顶堆的根节点依次和数组的最后一个,倒数第二个,倒数第三个......做交换,每次交换完后,需要从根节点到与之交换的那个结点之前的结点之间进行调整大顶堆,保证大顶堆的符合上述规则。
在完全二叉树中,如果用顺序结构来存储这棵树,那么某个结点和它左右孩子结点之间存在以下关系(层序遍历):左孩子下标等于双亲结点下标的2倍,右孩子下标等于双亲结点2倍+1。
交换函数 void swap(int k[], int i, int j) { int temp = k[i]; k[i] = k[j]; k[j] = temp; }
调整大顶堆的函数
void HeapAdjust(int k[], int s, int n) //从s到n开始调整大顶堆,s表示待调整的结点 { int temp = k[s]; //保存当前需要调整的结点 for(int i = 2*s; i <= n; i*=2) //2*s表示s这个结点的左孩子,i*=2表示当前结点的左孩子结点,也就是下一个检查的结点,因为移动当前检查的结点后,可能会对其孩子结点的规则完整性破坏,所以需要往下检查 { if(i < n && k[i] < k[i+1]) //k[i]表示左孩子,k[i+1]表示右孩子,i<n是为了保证不是最后一个结点 { i++; //永远让i指向较大的孩子结点 } if(temp >= k[i]) //如果待调整的双亲大于两孩子中较大的孩子,则不需要调整 { break; } //下面将较大的更新为双亲结点 k[s] = k[i]; s=i; } k[s] = temp; } /** 对上面for循环做一个解释,当检查到较上的结点时候,移动后不能保证树的规则, 应该继续检查其孩子结点,因为做了交换后可能会破坏孩子结点的大顶堆规则 */对堆排序的实现
为了方便起见,数组不用第0号元素,从第一号元素开始。
假设一共n个结点,第n/2个结点刚好是最后一个拥有孩子结点的结点,这个也是完全二叉树的规律,而初始我们就应该从下往上去检查,因为上面的结点是根据下面的结点检查的。
(从小到大排列)直接插入排序就是:遍历这个数组,然后如果发现后一个比前一个小,则将后一个较小的拿出来,记为x,然后与前面的依次作比较,如果比x大,则将其向后退一个位置,直到碰到一个比x小的元素,则将x放到它的后面即可,这样等到遍历完这个数组后,它就会变成有序的。
下面是一次外层循环的演示,对整个数组遍历一遍,作如下操作则可