五大常见算法策略之——动态规划策略（Dynamic Programming） (2)

  又是那只熟悉的青蛙，和上节递归与分治中相同的例题，一只青蛙一次可以跳上1级台阶，也可以跳上2级，求该青蛙跳上一个n级的台阶共有多少种跳法。详细思路可以看看上一篇文章——递归与分治策略。
我们下面先回顾一下上次用的递归算法：

public static int Jump_Floor1(int n){ if(n <= 2){ return n; }else{ //这里涉及到两种跳法，1、第一次跳1级就还有n-1级要跳，2、第一次跳2级就还有n-2级要跳 return Jump_Floor1(n-1)+Jump_Floor1(n-2); } }

其实和第一个例子斐波那契一样，之所以把它又拉出来讨论，是因为它的递归解法中涉及的重复计算实在太多了，我们需要将已经计算过的数据保存起来，以避免重复计算，提高效率。这里大家可以先自己试着改一下其实和第一个例子的改进方法是一样的，用一个数组来缓存计算过的数据。

/** * 看完递归的方法不要先被它的代码简洁所迷惑，可以分析一下复杂度，就会发现有很多重复的计算 * 而且看完这个会发现和Fibonacci的递归方法有点像 * @非递归 */ private static int result[] = new int[100]; public static int Jump_Floor2(int n){ if(n <= 2){ return n; }else{ if(result[n] != 0) return result[n]; else{ result[n] = Jump_Floor2(n-1)+Jump_Floor2(n-2); return result[n]; } } }

下面将难度做一提升，我们来讨论一道DP策略里的经典例题——最长公共子列问题

最长公共子序列问题

给定两个序列，需要求出两个序列最长的公共子序列，这里的子序列不同于字串，字串要求必须是连续的一个串，子序列并没有这么严格的连续要求，我们举个例子：

比如A = "LetMeDownSlowly!" B="LetYouDownQuickly!" A和B的最长公共子序列就是"LetDownly!"

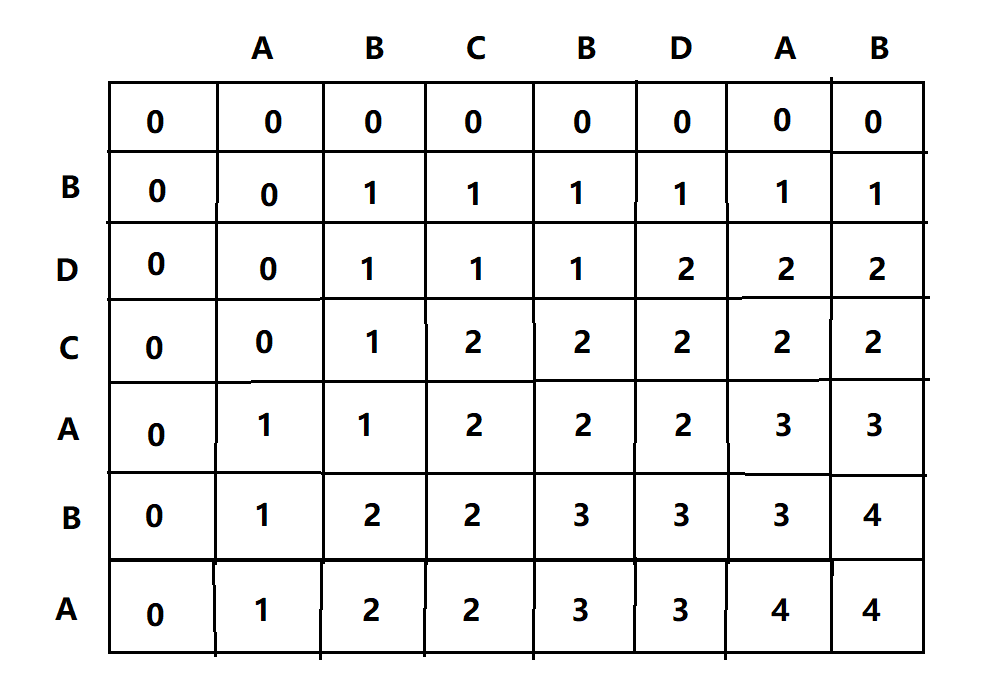
比如字符串1：BDCABA；字符串2：ABCBDAB，则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

我们设 X=(x1,x2,.....xn) 和 Y={y1,y2,.....ym} 是两个序列，将 X 和 Y 的最长公共子序列记为LCS(X,Y)，要找它们的最长公共子序列就是要求最优化问题，有以下几种情况：

1、n = 0 || m = 0，不用多说最长的也只能是0，LCS(n,m) = 0

2、X(n) = Y(m)，说明当前序列也是相等的，那就给这两个元素匹配之前的最长长度加一，即LCS(n,m)=LCS(n-1,m-1)+1

3、X(n) != Y(m)，这时候说明这两个元素并没有匹配上，那所以最长的公共子序列长度还是这两个元素匹配之前的最长长度，即max{LCS(n-1,m)，LCS(n,m-1)}
由此我们可以列出状态转移方程：（用的别人的图）

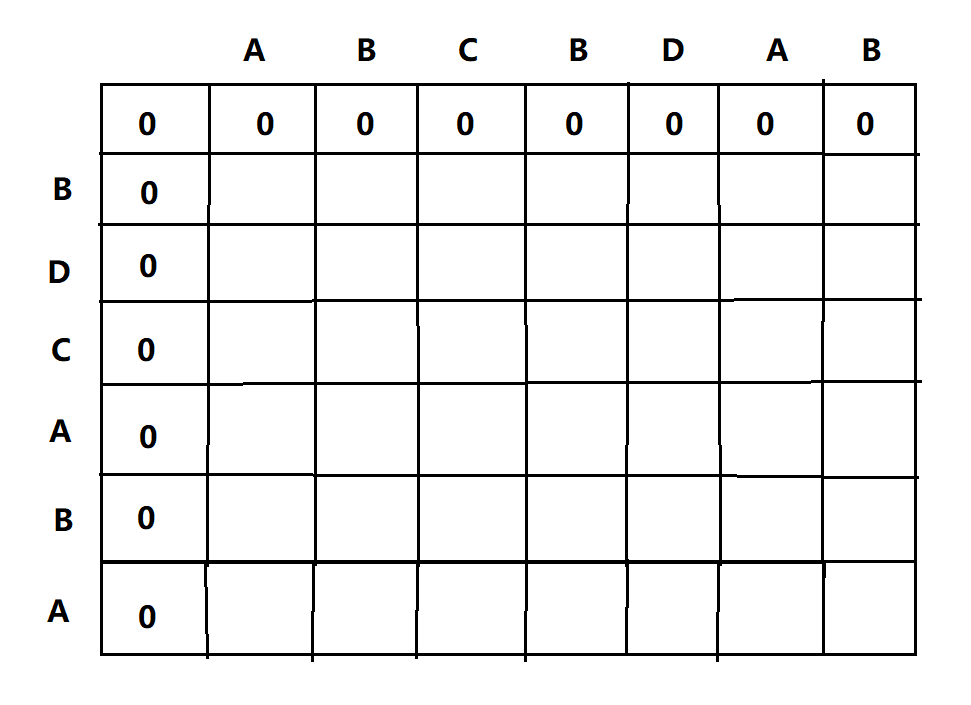
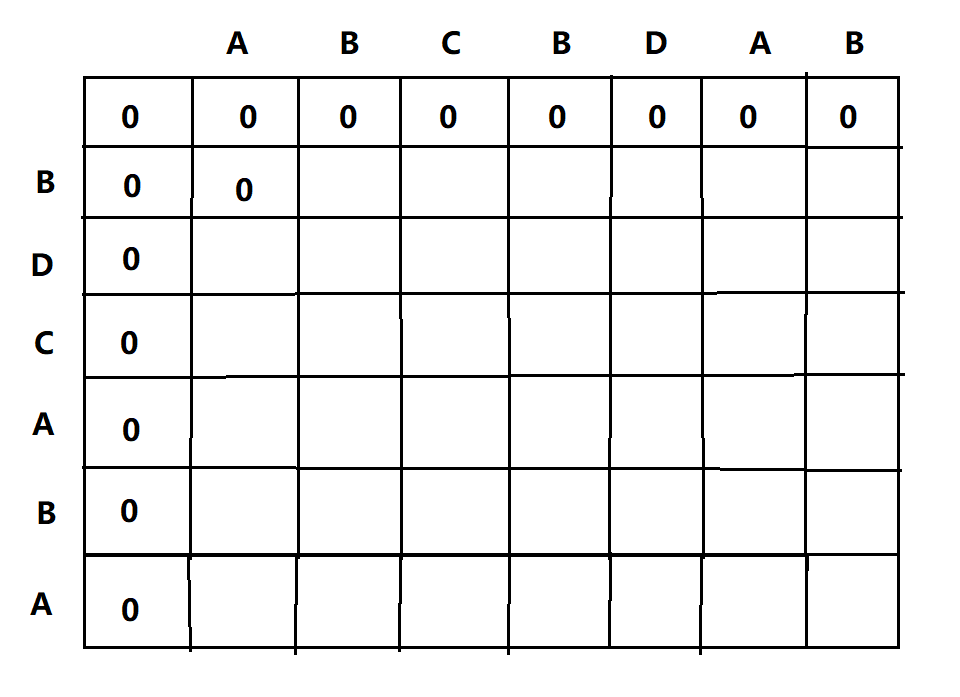
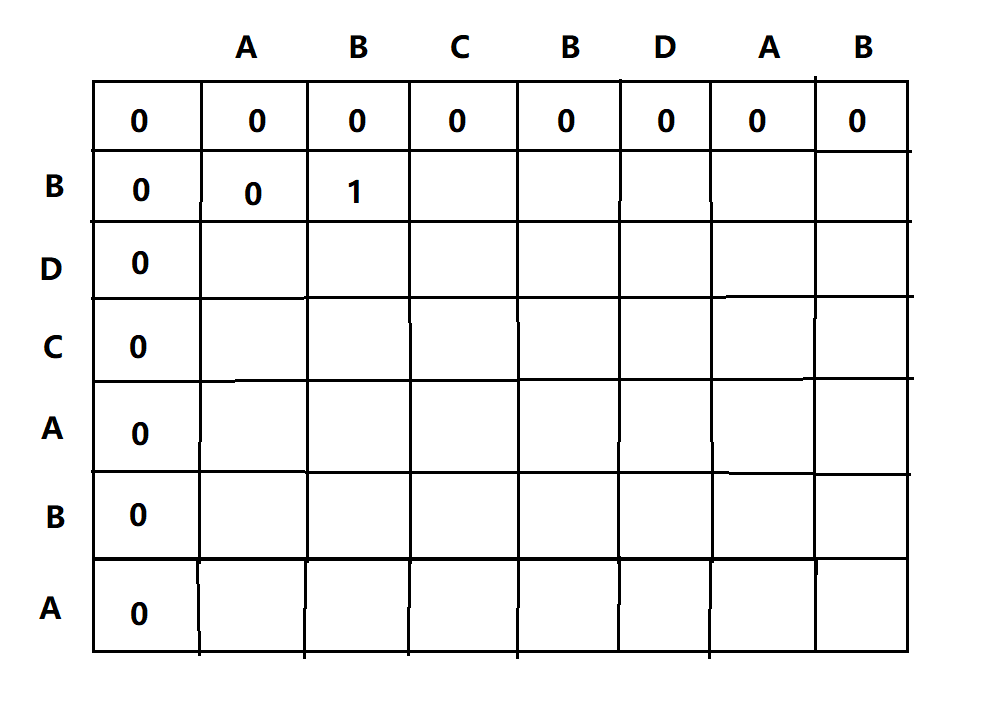
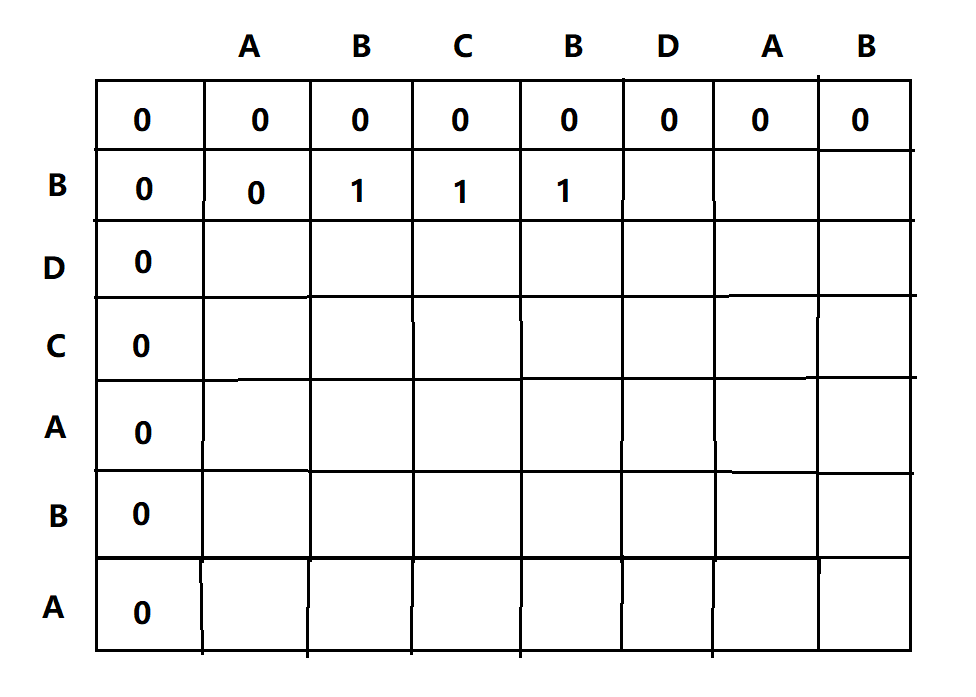
我们可以考虑用一个二维数组来保存LCS(n,m)的值，n表示行，m表示列，作如下演示，比如字符串1：ABCBDAB，字符串2：BDCABA；

1、先对其进行初始化操作，即将m=0，或者n=0的行和列的值全填为0

2、判断发现A != B，则LCS(1,1) = 0，填入其中

3、判断B == B，则LCS(1,2) = LCS(0,1)+1=1，填入其中

4、判断B != C，则LCS(1,3)就应该等于LCS(0,3)和LCS(1,2)中较大的那一个，即等于1，通过观察我们发现现在的两个序列是{B}和{ABC}在比较，即使现在B != C，但是因为前面已经有一个B和其匹配了，所以长度最少已经为1了，所以当C未匹配时，子序列的最大值是前面的未比较C和B时候的最大值，所以填1 5、再比较到B和B，虽然两者相等，但是只能是LCS(n-1,m-1)+1，所以还是1，因为一个B只能匹配一次啊，举个例子：就好像是DB和ABCB来比较，当第一个序列的B和第二个序列的第二个B匹配时，就应该是D和ABC的最长子序列+1，所以如下填表：

6、掌握规律后，我们直接完整填完这个表