canvas基础[一]探究出初中数学知识 (2)

arcTo

arcTo(x1,y1,x2,y2,radius)

画曲线,要想明白它们之间的关系需要画辅助线

let x0 = 100, y0 = 100, x1 = 400, y1 = 100, x2 = 350, y2 = 150; ctx.beginPath(); ctx.moveTo(x0, y0); ctx.strokeStyle = "#f00"; ctx.lineWidth = 2; ctx.arcTo(x1, y1, x2, y2, 20); ctx.stroke(); ctx.beginPath(); ctx.strokeStyle = "rgba(0,0,0,0.5)"; ctx.lineWidth = 1; ctx.moveTo(x0, y0); ctx.lineTo(x1, y1); ctx.fillText('x1,y1', x1 + 10, y1 + 10) ctx.lineTo(x2, y2); ctx.fillText('x2,y2', x2 + 10, y2) ctx.stroke();

说明一下,x0,y0 起点坐标,x1,y1 第一个点坐标,x2,y2 第二个坐标

arcTo的规律: 他其实是通过起点，第1点，第2点的两条直线，组成了一个夹角，而这两条线，也是参数圆的切线。其中圆的半径决定了圆会在什么位置与线条发生切边。

让我们把球球变大吧！

ctx.arcTo(x1,y1,x2,y2,50); //半径改成50

我们发现他们还是相切的,因为切线可以无限延长

为了方便计算，我先把两条线的夹角改成90度。

var x0=100,
y0=400,
x1 = 500,
y1 = 400,
x2 = 500,
y2 = 450;

更改后就是90度张开了哟！我们保持球的半径不变。刷新后：

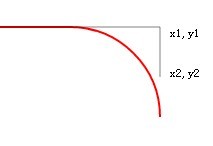
我们把y2变大，也就是延长了一条切线，把他变成550，刷新后：

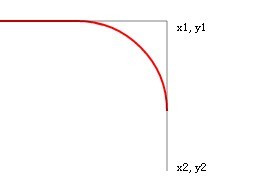
切线是延长了，但arcTo画出的红线没有任何变化。

写一个可行的案例吧

绘制一个背景网格

// 绘制网格 grid for (let x = 0.5; x < 500; x += 10) { ctx.moveTo(x, 0); ctx.lineTo(x, 500) } for (let y = 0; y < 500; y += 10) { ctx.moveTo(0, y) ctx.lineTo(500, y) } ctx.strokeStyle = '#eee'; ctx.stroke();

画两条直线相交

// lines ctx.strokeStyle = 'gray'; ctx.lineWidth = 1; ctx.beginPath() ctx.moveTo(51, 24) ctx.lineTo(314, 540) ctx.moveTo(477, 34) ctx.lineTo(86, 484) ctx.stroke();

绘制两条线上的点

问题来了两点确定一条直线怎么知道线上的点的位置关系

两点式公式
(y-y2)/(y1-y2) = (x-x2)/(x1-x2)

求两条直线上面的交点

function segmentsIntr(a, b, c, d){ //线段ab的法线N1 let nx1 = (b.y - a.y), ny1 = (a.x - b.x); //线段cd的法线N2 let nx2 = (d.y - c.y), ny2 = (c.x - d.x); //两条法线做叉乘, 如果结果为0, 说明线段ab和线段cd平行或共线,不相交 let denominator = nx1*ny2 - ny1*nx2; if (denominator==0) { return false; } //在法线N2上的投影 let distC_N2=nx2 * c.x + ny2 * c.y; let distA_N2=nx2 * a.x + ny2 * a.y-distC_N2; let distB_N2=nx2 * b.x + ny2 * b.y-distC_N2; // 点a投影和点b投影在点c投影同侧 (对点在线段上的情况,本例当作不相交处理); if ( distA_N2*distB_N2>=0 ) { return false; } // //判断点c点d 和线段ab的关系, 原理同上 // //在法线N1上的投影 let distA_N1=nx1 * a.x + ny1 * a.y; let distC_N1=nx1 * c.x + ny1 * c.y-distA_N1; let distD_N1=nx1 * d.x + ny1 * d.y-distA_N1; if ( distC_N1*distD_N1>=0 ) { return false; } //计算交点坐标 let fraction= distA_N2 / denominator; let dx= fraction * ny1, dy= -fraction * nx1; return { x: a.x + dx , y: a.y + dy }; } console.log(segmentsIntr({x: 51, y: 24}, {x: 314, y: 540}, {x: 477, y: 34}, {x: 86, y: 484}));

上demo代码

// 两点式公式 // (y-y2)/(y1-y2) = (x-x2)/(x1-x2)。 // 我们设y=200,可以求出x=140.7 ctx.beginPath() ctx.moveTo(140.7,200) ctx.arc(140.7,200,5,0,2*Math.PI) // 设x=350,求右边直线的y点 180.16 ctx.moveTo(350,180.16) ctx.arc(350,180.16,5,0,2*Math.PI) // 求原点坐标 ctx.moveTo(211.713,339.3166) ctx.arc(211.713,339.3166,5,0,2*Math.PI) ctx.fillStyle = 'red'; ctx.fill();

标记点的位置

ctx.font='14px Arial' ctx.beginPath() ctx.fillText("(x0,y0)",140.7+5,200+5) ctx.fillText("(x1,y1)",350+5,180.16+5) ctx.fillText("(x2,y2)",211.713+5,339.3166+5)

画arcTo 曲线

// 编写arcTo ctx.beginPath() ctx.lineWidth=3; ctx.moveTo(140.7,200) ctx.arcTo(211.713,339.3166,350,180.16,100) ctx.stroke()