np.tile可以对目标操作数组进行广播扩展,比如 1x3 如下操作可以广播为 4x6,注意与前面所说的broadcast_to进行区别,broadcast_to必须要扩维,而tile可扩维,也可不扩维,具体操作根据自己的实际需求进行。
有过Tensorflow经验的读者应该知道,其内部也有tile和broadcast操作,但是当我们的数据量比较大的时候,据说tile的效率比broadcast要低,暂时还没了解原因,以后有用到在了解吧。
In [20]: a Out[20]: array([[1, 1, 0]]) In [21]: np.tile(a, [4, 2]) # 第二个参数表示各个维度广播的倍数,这里表示的是行扩4倍,列扩2倍 Out[21]: array([[1, 1, 0, 1, 1, 0], [1, 1, 0, 1, 1, 0], [1, 1, 0, 1, 1, 0], [1, 1, 0, 1, 1, 0]])关于NumPy中的复制和试图:这个部分的知识也是我之前在学习NumPy时候所遗漏的点,趁着这个机会,把它在这记录一下。
没有复制
关于这一点,其实在之前记录算法的时候同样提到过,这一点还是需要格外注意的。
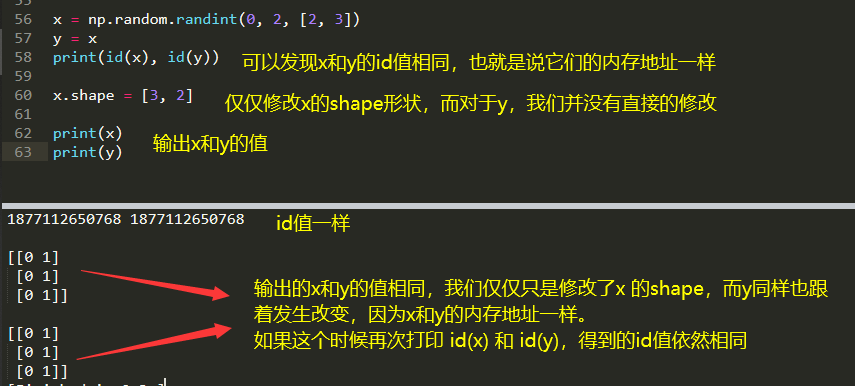
视图或者浅拷贝(view)
同样采用上面一样的代码,仅仅修改了第57行,将 y = x 和 y = x.view(),可以发现,此时的x和y的id值不一样,也就是说他们的内存地址不一样,我们修改x的shape之后,y的shape并没有发生改变。
但是,当我们改变不是shape,而是改一个变数组内部的数据,则另一个数组同样会发生改变

副本或者深拷贝(copy)
视图或者浅拷贝采用的是view,而副本或者深拷贝采用的是copy。使用copy的时候无论是修改一个数组的shape,还是内部元素,另一个数组都不会发生改变。
(关于copy,这里就不再演示代码了,读者可自行操作,然后进行比较)
最后总结一下:
y = x,说明x和y的内存地址相同,修改其中一个,另一个也会随着发生改变(无论是shape,还是内部元素)
y = x.view(),两者的内存地址不一样,修改其中一个的shape,另一个不会发生改变;而修改其中一个元组的内部元素,则另外一个会跟着发生改变
y = x.copy(),两者的内存地址不一样,无论是修改一个元组的shape,还是内部元素,另外一个都不会发生改变,两者相互独立
NumPy中的数学相关函数,这部分内容没什么好讲的:
np.pi,返回π值
np.sin(),返回正弦值
np.cos(),返回余弦值
np.tan(),返回正切值
numpy.ceil(),返回大于或者等于指定表达式的最小整数,即向上取整。
np.exp(2),返回指数值,也就是 $e^2$
其他相关数学函数,可参考官方文档。
NumPy中的算术运算,这部分内容也没什么好讲的:
numpy.add(a,b):两数组相加
numpy.subtract(a,b):两数组相减
numpy.multiply(a,b):两数组相乘
numpy.divide(a,b):两数组相除
numpy.reciprocal(a),返回倒数
numpy.power(a, 4),返回a的四次方
NumPy中的统计函数,这个稍微记录一下:
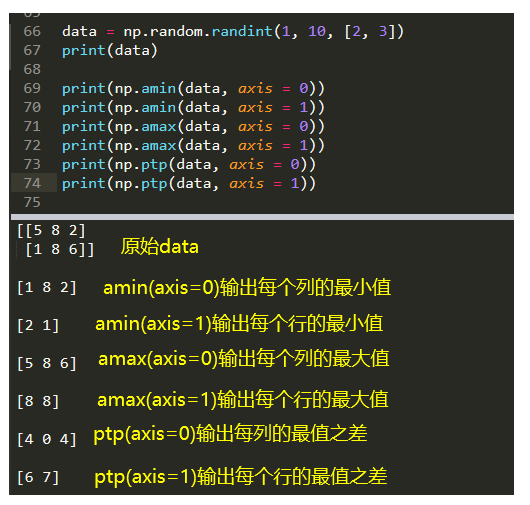
以上示例了在数组中获取最值以及最值之差的方式,传入了axis参数,则按照对应方向获取,假如没有传入axis参数,则表示获取数组整体的最值。除了以上几个接口之外,还有其他一些常见的统计函数,具体操作和上述并无一二,如下:
np.amin():获取最小值
np.amax():获取最大值
np.ptp():获取最值之差
np.median():获取中位数(中值)
np.mean():获取均值
np.var():获取方差,$\sigma^2 = \frac{1}{n}\sum_{i=1}n(x_i-\overline{x})2$
np.std():获取标准差,$\sigma$
NumPy中的线性代数:
np.dot(a, b) 就是两个矩阵的乘积
np.vdot(a, b) 两个矩阵对应位置数的乘积之和
np.inner(a, b) 內积,就是a的每行与b的每行相乘求和
比如a=[[1, 0], [1, 1]],b=[[1, 2], [1, 3]]
np.inner(a, b)相当于[1, 0] * [1, 2] = 1 -> 为第一个数
[1, 0] * [1, 3] = 1 -> 为第二个数
[1, 1] * [1, 2] = 3 -> 为第三个数
[1, 1] * [1, 3] = 4 -> 为第四个数
矩阵乘积就是第一个矩阵的行与第二个矩阵的列乘积之和,而inner相当于第一个矩阵和第二个矩阵的行乘积之和
np.matmul(a, b) 目前感觉和np.dot(a, b)作用一样,都是矩阵乘积
np.linalg.det(a) 计算矩阵的行列式的值
np.linalg.solve(a, [[1], [1]]) 求线性方程组的解,第一个的参数相当于系数,第二个参数相当于参数项
np.linalg.inv(a) 计算矩阵的逆矩阵
# 将数组保存到以 .npy 为扩展名的文件中。 numpy.save(file, arr, allow_pickle=True, fix_imports=True)file:要保存的文件,扩展名为 .npy,如果文件路径末尾没有扩展名 .npy,该扩展名会被自动加上。
arr: 要保存的数组

