再通过我们之前得出的性质:土地高度\(y\)随着下标的增大而减小,以及花费\(f_j\)满足随着\(j\)的增大而增大,可以画出如下图像。
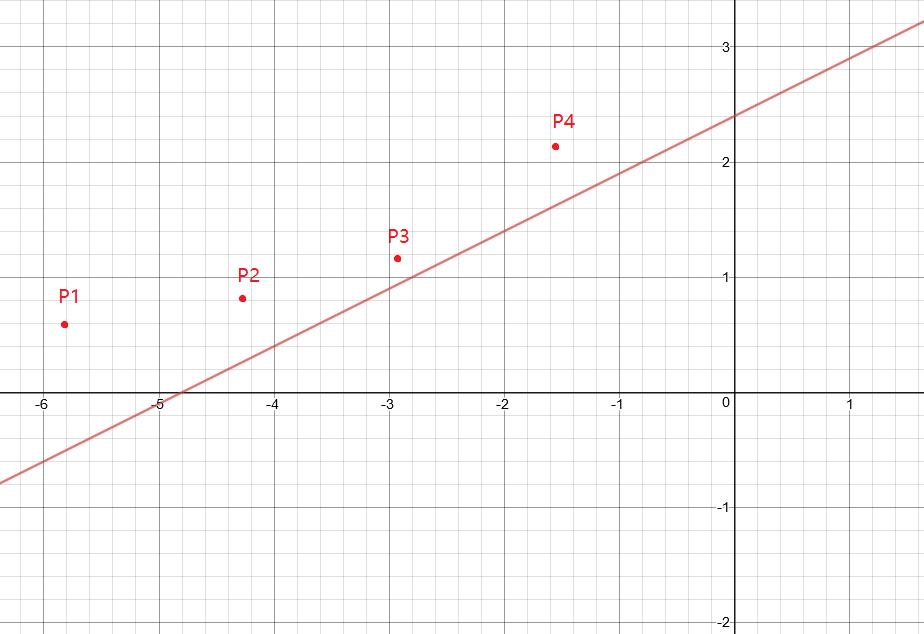
满足斜率为\(x_i\)的直线自上向下移动,由于我们需要截距\(f_i\)最小,当他碰到第一个\(P_j\)时,我们便得到了最优决策\(j\)。
注意到\(x_i\)满足单调上升,\(P\)点围成的凸包的两两节点之间的斜率也满足单调递增,就可以得到如下性质。
1.\(slope(P_j,P_{j+1})>x_i\)且\(slope(P_{j-1},P_j)<x_i\)时,\(j\)为最优决策,否则\(j\)永远不会成为最优决策
2.\(slope(P_x,P_y)<slope(P_x,P_{y'})\),决策\(y'\)优于\(y\)
确认其具有如上性质后,单调队列维护即可。
STEP 5: 代码实现确立作法后,我们需要代码实现
注意事项
1.斜率函数中的斜率满足单调递增(递减)时,可以使用单调队列维护,转移均摊时间复杂度\(O(1)\)
2.斜率函数中的斜率不满足单调递增(递减),但满足两两节点之间的斜率单调递增的凸包存在时(即性质\(2\)有效时),可以使用单调栈维护,二分查找找到最优决策,转移均摊时间复杂度\(O(log_2n)\)
3.\(slope\)函数的返回值为\(double\)类型
4.注意是否需要开长整型变量\((longlong)\)
\(Code:\)
#include<bits/stdc++.h> using namespace std; const int N=50000+80; struct earth{long long x,y;}a[N],Stack[N],d[N]; long long n,top=0,f[N],q[N*2],head=1,tail=1; inline bool cmp(earth p1,earth p2){if(p1.x==p2.x)return p1.y<p2.y;else return p1.x<p2.x;} inline void input(void) { scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].x,&a[i].y); } inline void init(void) { sort(a+1,a+n+1,cmp); for(int i=1;i<=n;i++) { while(top&&Stack[top].y<=a[i].y)top--; Stack[++top]=a[i]; } for(int i=1;i<=top;i++) { d[i]=Stack[i]; } sort(d+1,d+top+1,cmp); } inline double slope(long long p,long long q){return (f[q]-f[p])*1.0/(d[p+1].y-d[q+1].y);} inline void dp(void) { f[0]=0; for(int i=1;i<=top;i++) { while(head<tail&&slope(q[head],q[head+1])<d[i].x)head++; f[i]=f[q[head]]+d[q[head]+1].y*d[i].x; while(head<tail&&slope(q[tail-1],q[tail])>slope(q[tail-1],i))tail--; q[++tail]=i; } } int main(void) { input(); init(); dp(); printf("%lld\n",f[top]); }
