采用分治策略,可将所有参加比赛的选手分成两部分,n=2^k 个选手的比赛日程表就可以通过n=2^(k-1) 个选手的的比赛日程表来决定。递归的执行这样的分割,直到只剩下两个选手,比赛日程表的就可以通过这样的分治策略逐步构建。
说个大白话就是:先默认构造日程表第一行,即0,1,2,3,...然后先分割日程表,将左上角复制到右下角,右上角复制到左下角
初始化第一行不做赘述,让chess[0][i] = i+1即可
下面在Excel中用图示做一演示
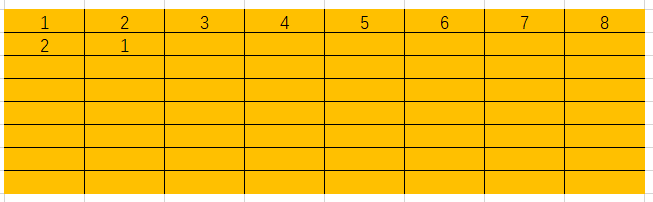
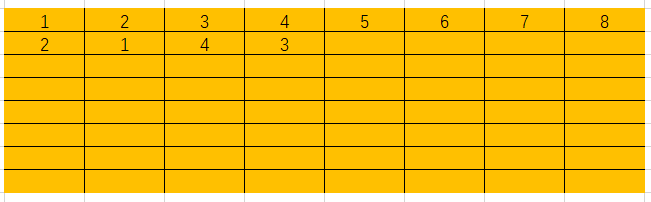
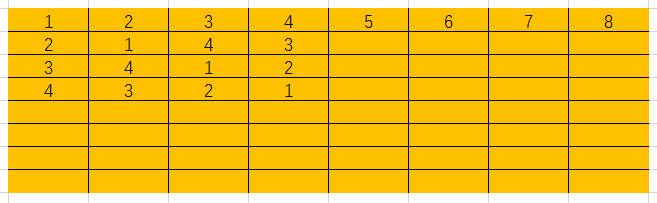
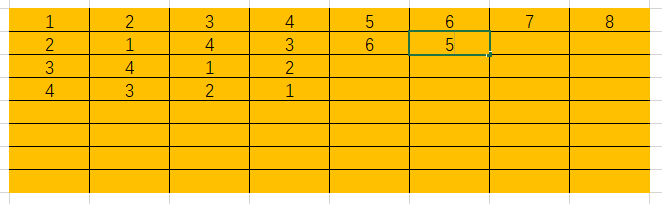
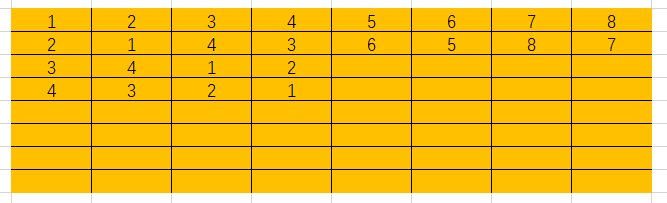
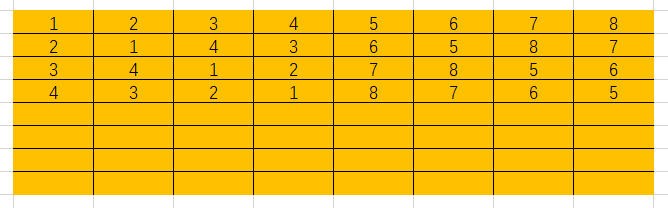

代码实现
/** * 将比赛日程表设计成n行n列,表中除了第一列,其他n-1列才是我们要的,数组下标行列都从0开始,第i行j列代表第(i+1)位选手在第j天的对手: * 表格初始化会将第一行按1到n一次填充,然后递归填充下面的,用左上角和右上角分别去填充右下角和左下角,因为要是对称矩阵(具体原因好好想想) * @param p 表示行序号 * @param q 表示列序号 * @param t 表示当前传进函数方格的规模也就是大小 * @param arr 表格 */ public static void arrange(int p, int q, int t, int arr[][]){ if(t>=4){ //如果规模大于4,就继续递归 arrange(p,q,t/2,arr); arrange(p,q+t/2,t/2,arr); } //填左下角 for(int i=p+t/2;i<p+t;i++){ for(int j=q;j<q+t/2;j++){ arr[i][j]=arr[i-t/2][j+t/2]; } } //填右下角 for(int i=p+t/2;i<p+t;i++){ for(int j=q+t/2;j<q+t;j++){ arr[i][j]=arr[i-t/2][j-t/2]; } } }
