程序猿修仙之路--算法之快速排序到底有多快 (2)

2.   key首先与arr[right]进行比较，如果arr[right]<key，则arr[left]=arr[right]将这个比key小的数放到左边去，如果arr[right]>key则我们只需要将right--，right--之后，再拿arr[right]与key进行比较，直到arr[right]<key交换元素为止。

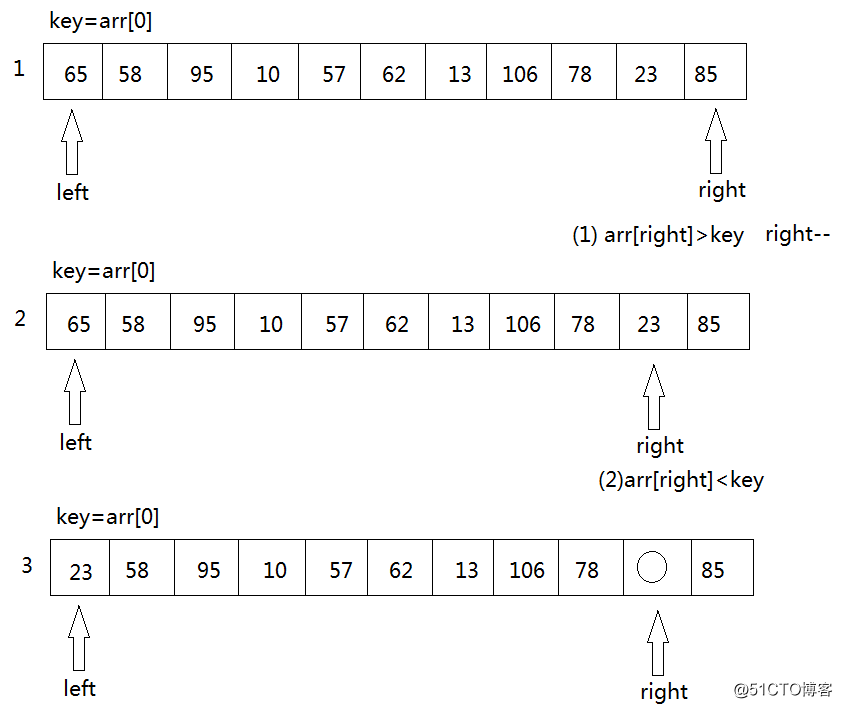
3.   如果右边存在arr[right]<key的情况，将arr[left]=arr[right]，接下来，将转向left端，拿arr[left ]与key进行比较，如果arr[left]>key,则将arr[right]=arr[left]，如果arr[left]<key，则只需要将left++,然后再进行arr[left]与key的比较。

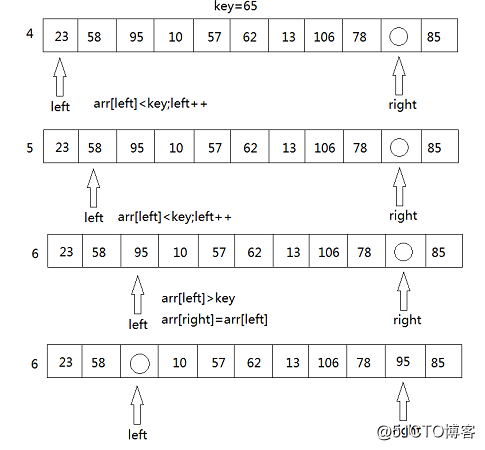
4.   然后再移动right重复上述步骤

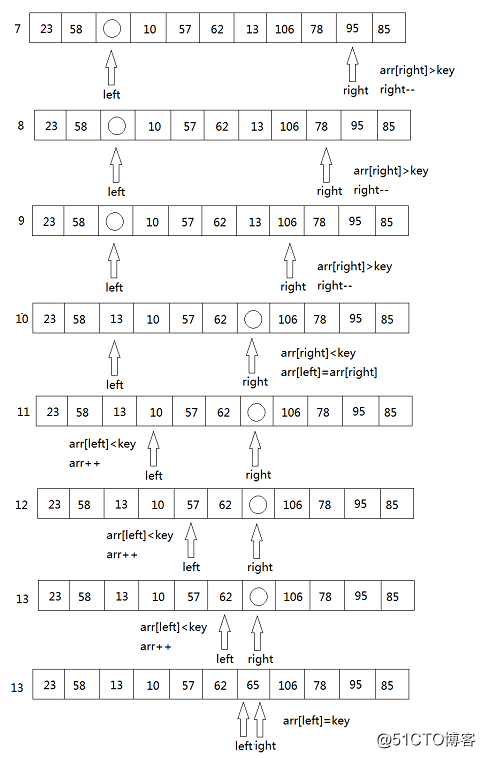
5.   最后得到 {23 58 13 10 57 62} 65 {106 78 95 85}，再对左子数列与右子数列进行同样的操作。最终得到一个有序的数列。

{23 58 13 10 57 62} 65 {106 78   95 85}

{10 13} 23 {58 57 62} 65 {85 78 95} 106

10 13 23 57 58 62 65 78 85 95 106

性能特点 关于复杂度相关O（n）等公式，我这里需要强调一点,公式代表的是算法的复杂度增长的趋势，而不是具体计算复杂度的公式。比如：O（n²）和O（n）相比较，只是说明 O(n²)增长的趋势要比o(n)快，并不是说明O(n²)的算法比O(n)的算法所用时间一定就要多。

1. 时间复杂度：

        快速排序平均时间复杂度为O(nlogn),最好情况下为O(nlogn)，最坏情况下O(n²)

2. 空间复杂度：

        基于以上例子来实现的快排，空间复杂度为O(1),也就是原地排序。

 3. 稳定性：

        举个例子：待排序数组:int a[] ={1, 2, 2, 3, 4, 5, 6};在快速排序的随机选择比较子(即pivot)阶段：若选择a[2]（即数组中的第二个2）为比较子，，而把大于等于比较子的数均放置在大数数组中，则a[1]（即数组中的第一个2）会到pivot的右边， 那么数组中的两个2非原序（这就是“不稳定”）。

若选择a[1]为比较子，而把小于等于比较子的数均放置在小数数组中，则数组中的两个2顺序也非原序。可见快速排序不是稳定的排序。

改进 通过以上分析各位侠士是否能够分析出来快速排序有哪些地方存在瑕疵呢？

1. 切分不平衡：

        也就是说我们选取的切分元素距离数组中间值的元素位置很远，极端情况下会是数组最大或最小的元素，这就导致了划分出来的大数组会被划分为很多次。针对此情况，我们可以取数组多个元素来平衡这种情况，例如：我们可以随机选取三个或者五个元素，取其中间值的元素作为分割元素。

2. 小数组：

        当快速排序切分为比较小的数组时候，也会利用递归调用自己。在这种小数组的情况下，其实一些基础排序算法反而比快速排序要快。当数组比较小的时候不妨尝试一下切换到插入排序。具体多小是小呢？一般5-15吧，仅供参考。

3. 重复元素：

        在我们实际应用中经常会遇到重复元素比较多的情况，按照快排的思想，相同元素是会被频繁移动和划分的，其实这完全没有必要。我们该怎么办呢？我们可以把数组切换为三部分：大于-等于-小于 三部分数组，这样等于的那部分数组就可以避免移动了，不过落地的代码复杂度要高很多，有兴趣的同学可以实现一下。

使用场景

1. 当一个数组大小为中型以上的数量级时，菜菜认为可以使用快速排序，并且伴随着数组的持续增大，快速排序的性能趋于平均运行时间。至于多大的数组为中型，一般认为50+ 吧，仅供参考。