看出来没,函数I的运算规则正好和对数的运算规则相同:
所以我们的函数可以用对数函数,最终我们给出信息量的量化公式:设事件A发生的概率为p,则事件A发生了带给我们的信息量为logb(1/p),式中的b是对数的底,b的取值决定信息量的单位,如b取2信息量的单位是bit,b取自然常数e信息量的单位是nat,容易计算1 nat=log2e≈1.443 bit1 nat=log2e≈1.443 bit (2)期望
概率论中描述一个随机事件中的随机变量的平均值的大小可以用数学期望这个概念,数学期望的定义是实验中可能的结果的概率乘以其结果的总和
举个简单的例子:
小时候玩的自动吐硬币的赌博机,硬币Y遵从以下概率分布,吐0个币的概率为0.7,吐10个币的概率为0.29,吐20个币的概率为0.01,那么Y的期望值为:
E[Y] = 0*0.7 + 10 * 0.29 + 20 * 0.01
(3)熵熵很难理解,拿书本上的一句话说,它们自从诞生的那一天起,就注定令世人十分费解。但是只要记住熵定义为信息的期望值,理解信息和期望后,使用熵也就不费解了
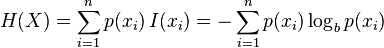
Gain(S,Sv) = H(S)- (|Sv|/|S|)H(Sv)
信息增益 = 经验熵 - 条件熵
用通俗的话理解就是,当加入了一个判断条件之后,我需要判定一个结论所需要的信息熵相比之前就有所减少了,这减少的量就是信息增益
3. 决策树构造实现 3.1 需求比如现在海洋中有5种生物,我们根据(不浮出水面是否可以生存,是否有脚蹼(鱼尾中间的薄膜))两个分类特征来判断该生物是否属于鱼类来构建决策树
看下表:
浮出水面是否可以生存 是否有脚蹼 属于鱼类1 否 是 是
2 否 是 是
3 否 否 否
4 是 是 否
5 是 是 否
3.2 构思
(1)伪代码的创建
前面说决策树在本质上就是一组嵌套的if-else判断规则树,那么我有个疑惑:面对这么多规则,我该先选哪个规则作为第一规则,再选哪个作为第二规则呢?规则选择次序不同,对决策树的构造会有什么影响?
这两个问题就涉及到了自信息的概念,一个规则给我们提供的信息量究竟有多大,信息量越大我们肯定能最快的得到想要的答案,从而决策树的高度也会最大程度的小
由此,我们首先需要判断数据集上的哪个规则在划分数据分类时起决定性作用,然后再对数据集进行划分,创建分支的伪代码如下:
if so return 类标签 else 寻找到分类数据种的最好特征 划分数据集 创建分支节点 for 每个划分的子集 递归 return 分支节点

