Ceres Solver: 高效的非线性优化库（二）实战篇 (2)

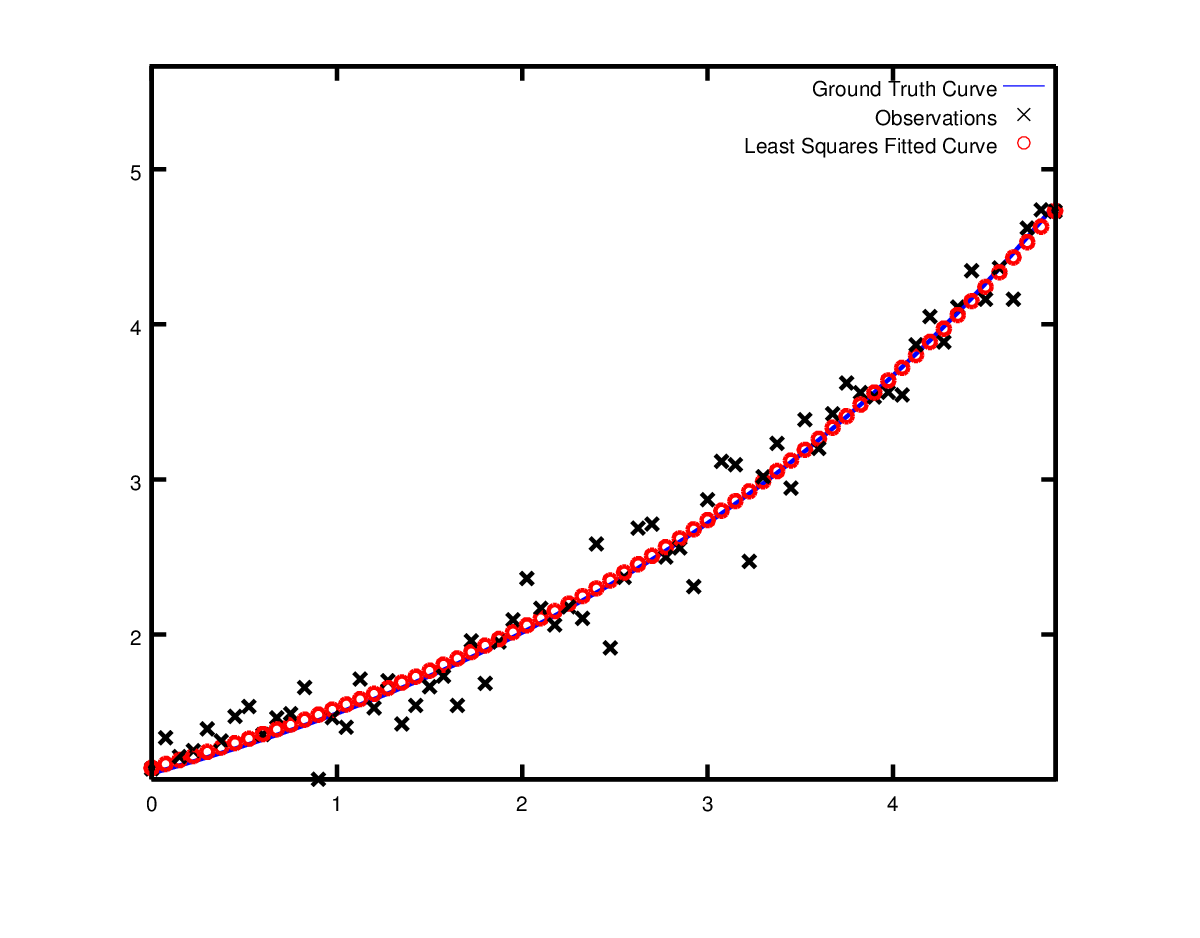
之前的例子都是不依赖数据的简单例子。非线性最小二乘法分析最初的目标是把数据拟合称曲线。现在考虑曲线拟合的数据，公式为\(y = e^{0.3x + 0.1}\)。对其进行采样并加入方差为\(\sigma = 0.2\)高斯噪声。我们希望拟合曲线
\[ y = e^{mx + c} \]
首先我们定义一个模板对象来评估残差。

struct ExponentialResidual { ExponentialResidual(double x, double y) : x_(x), y_(y) {} template <typename T> bool operator()(const T* const m, const T* const c, T* residual) const { residual[0] = T(y_) - exp(m[0] * T(x_) + c[0]); return true; } private: // Observations for a sample. const double x_; const double y_; };

假设我们有观测数据\(2n\)大小，构建如下问题。

double m = 0.0; double c = 0.0; Problem problem; for (int i = 0; i < kNumObservations; ++i) { CostFunction* cost_function = new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>( new ExponentialResidual(data[2 * i], data[2 * i + 1])); problem.AddResidualBlock(cost_function, NULL, &m, &c); }

变异运行examples/curve_fitting.cc得到相应结果。

iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time 0 1.211734e+02 0.00e+00 3.61e+02 0.00e+00 0.00e+00 1.00e+04 0 5.34e-04 2.56e-03 1 1.211734e+02 -2.21e+03 0.00e+00 7.52e-01 -1.87e+01 5.00e+03 1 4.29e-05 3.25e-03 2 1.211734e+02 -2.21e+03 0.00e+00 7.51e-01 -1.86e+01 1.25e+03 1 1.10e-05 3.28e-03 3 1.211734e+02 -2.19e+03 0.00e+00 7.48e-01 -1.85e+01 1.56e+02 1 1.41e-05 3.31e-03 4 1.211734e+02 -2.02e+03 0.00e+00 7.22e-01 -1.70e+01 9.77e+00 1 1.00e-05 3.34e-03 5 1.211734e+02 -7.34e+02 0.00e+00 5.78e-01 -6.32e+00 3.05e-01 1 1.00e-05 3.36e-03 6 3.306595e+01 8.81e+01 4.10e+02 3.18e-01 1.37e+00 9.16e-01 1 2.79e-05 3.41e-03 7 6.426770e+00 2.66e+01 1.81e+02 1.29e-01 1.10e+00 2.75e+00 1 2.10e-05 3.45e-03 8 3.344546e+00 3.08e+00 5.51e+01 3.05e-02 1.03e+00 8.24e+00 1 2.10e-05 3.48e-03 9 1.987485e+00 1.36e+00 2.33e+01 8.87e-02 9.94e-01 2.47e+01 1 2.10e-05 3.52e-03 10 1.211585e+00 7.76e-01 8.22e+00 1.05e-01 9.89e-01 7.42e+01 1 2.10e-05 3.56e-03 11 1.063265e+00 1.48e-01 1.44e+00 6.06e-02 9.97e-01 2.22e+02 1 2.60e-05 3.61e-03 12 1.056795e+00 6.47e-03 1.18e-01 1.47e-02 1.00e+00 6.67e+02 1 2.10e-05 3.64e-03 13 1.056751e+00 4.39e-05 3.79e-03 1.28e-03 1.00e+00 2.00e+03 1 2.10e-05 3.68e-03 Ceres Solver Report: Iterations: 13, Initial cost: 1.211734e+02, Final cost: 1.056751e+00, Termination: CONVERGENCE Initial m: 0 c: 0 Final m: 0.291861 c: 0.131439

使用初值\(m=0, c=0\), 初始目标函数值为\(121.173\)。Ceres计算得到\(m=0.291, c=0.131\).目标函数值为\(1.056\)。但这同原始模型不一样，但也是合理的。通过带噪声的数据恢复模型会得到一定的偏差。实际上，即使使用原始模型数据，偏差更大。

实战之曲线鲁棒拟合