推广到m个训练数据,参数更新公式为:
三、逻辑回归模型
逻辑回归与线性回归同属广义线性模型,逻辑回归是以线性回归为理论支持,是一个二分类模型,也可以推广多到分类问题,通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题,首先介绍一下Sigmoid函数:
sigmoid函数图像是一个S曲线,取值在[0, 1]之间,在远离0的地方函数的值会很快接近0或者1,sigmoid函数的求导特性是:
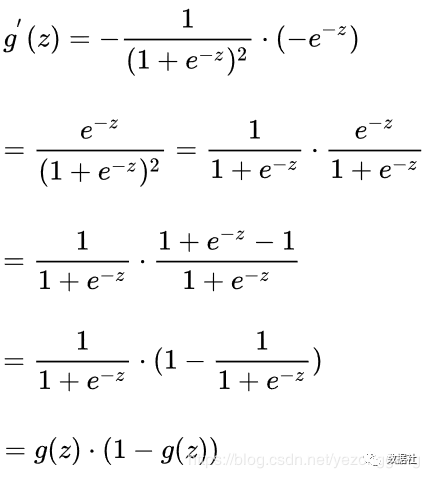
逻辑回归的预测函数是下图,只是在特征到结果的映射中加入了一层函数映射,先把特征线性求和,然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0到1之间:
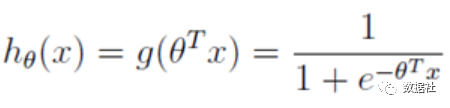
通过求似然函数,两边取log后,对θ求偏导:
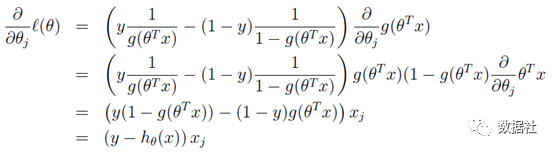
发现同线性回归模型是同一个表达式,这并不仅仅是巧合,两者存在深层的联系;
四、回归模型使用
数据是2014年5月至2015年5月美国King County的房屋销售价格以及房屋的基本信息。数据分为训练数据和测试数据,分别保存在kc_train.csv和kc_test.csv两个文件中,其中训练数据主要包括10000条记录,14个字段:销售日期,销售价格,卧室数,浴室数,房屋面积,停车面积,楼层数,房屋评分,建筑面积,地下室面积,建筑年份,修复年份,纬度,经度。
数据集地址:https://github.com/yezonggang/house_price,按照流程完成模型建立:
import pandas as pd from pandas import DataFrame import numpy as np import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns from sklearn.linear_model import LogisticRegression from sklearn.ensemble import RandomForestClassifier from sklearn.linear_model import LinearRegression # 数据读取 baseUrl="C:\\Users\\71781\\Desktop\\2020\\ML-20200422\\houre_price\\" house_df=pd.read_csv(baseUrl+'train.csv' ) test_df=pd.read_csv(baseUrl+'test.csv') house_df.head() # 删除无关变量 house_df=house_df.drop(['saleTime','year','repairYear','latitude','longitude','buildingSize'],axis=1) test_df=test_df.drop(['saleTime','year','repairYear','latitude','longitude','buildingSize'],axis=1) # 模型建立 X_price=house_df.drop(['price'],axis=1) # X_price.head() Y_price=house_df['price'] Y_price.head() LR_reg=LinearRegression() LR_reg.fit(X_price, Y_price) Y_pred = LR_reg.predict(test_df) LR_reg.score(X_price, Y_price) # 可以选择进行特征缩放 #new_house=house_df.drop(['price'],axis=1) #from sklearn.preprocessing import MinMaxScaler #minmax_scaler=MinMaxScaler().fit(new_house) #进行内部拟合,内部参数会发生变化 #scaler_housing=pd.DataFrame(minmax_scaler.transform(new_house),columns=new_house.columns) #mm=MinMaxScaler() #mm.fit(test_df) #scaler_t=mm.transform(test_df) #scaler_t=pd.DataFrame(scaler_t,columns=test_df.columns)

