重复二的操作,直到所有点都确定。
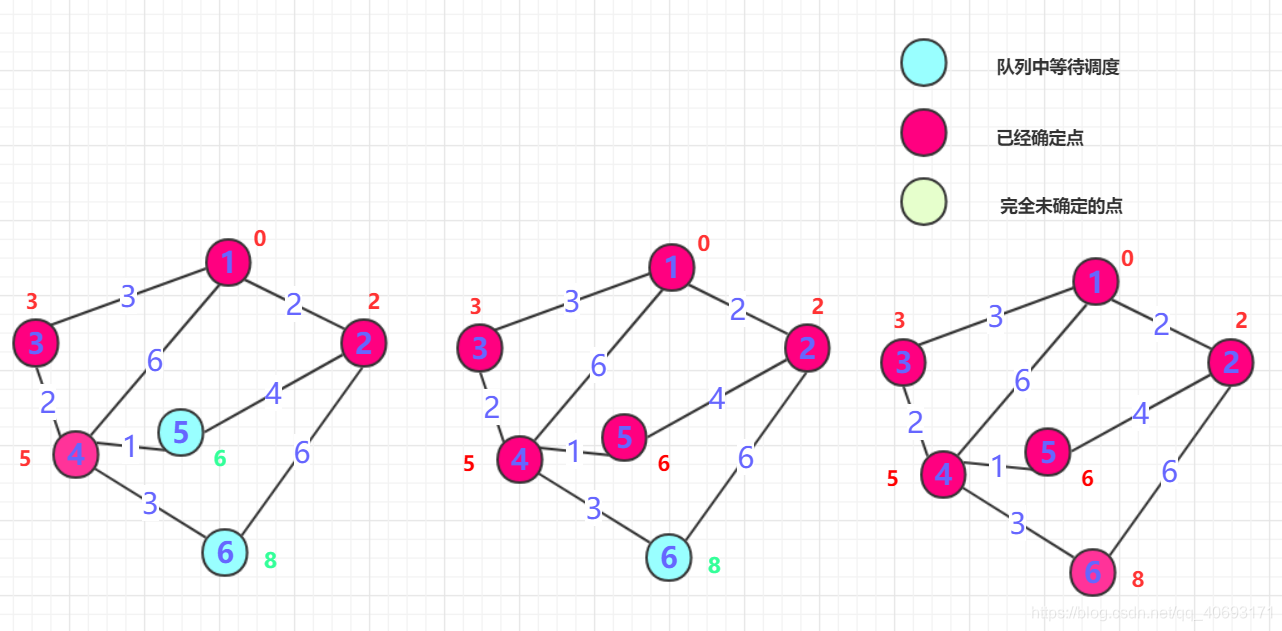
算法实现
package 图论;
import java.util.ArrayDeque;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class dijkstra {
static class node
{
int x; //节点编号
int lenth;//长度
public node(int x,int lenth) {
this.x=x;
this.lenth=lenth;
}
}
public static void main(String[] args) {
int[][] map = new int[6][6];//记录权值,顺便记录链接情况,可以考虑附加邻接表
initmap(map);//初始化
boolean bool[]=new boolean[6];//判断是否已经确定
int len[]=new int[6];//长度
for(int i=0;i<6;i++)
{
len[i]=Integer.MAX_VALUE;
}
Queue<node>q1=new PriorityQueue<node>(com);
len[0]=0;//从0这个点开始
q1.add(new node(0, 0));
int count=0;//计算执行了几次dijkstra
while (!q1.isEmpty()) {
node t1=q1.poll();
int index=t1.x;//节点编号
int length=t1.lenth;//节点当前点距离
bool[index]=true;//抛出的点确定
count++;//其实执行了6次就可以确定就不需要继续执行了 这句可有可无,有了减少计算次数
for(int i=0;i<map[index].length;i++)
{
if(map[index][i]>0&&!bool[i])
{
node node=new node(i, length+map[index][i]);
if(len[i]>node.lenth)//需要更新节点的时候更新节点并加入队列
{
len[i]=node.lenth;
q1.add(node);
}
}
}
}
for(int i=0;i<6;i++)
{
System.out.println(len[i]);
}
}
static Comparator<node>com=new Comparator<node>() {
public int compare(node o1, node o2) {
return o1.lenth-o2.lenth;
}
};
private static void initmap(int[][] map) {
map[0][1]=2;map[0][2]=3;map[0][3]=6;
map[1][0]=2;map[1][4]=4;map[1][5]=6;
map[2][0]=3;map[2][3]=2;
map[3][0]=6;map[3][2]=2;map[3][4]=1;map[3][5]=3;
map[4][1]=4;map[4][3]=1;
map[5][1]=6;map[5][3]=3;
}
}
执行结果:
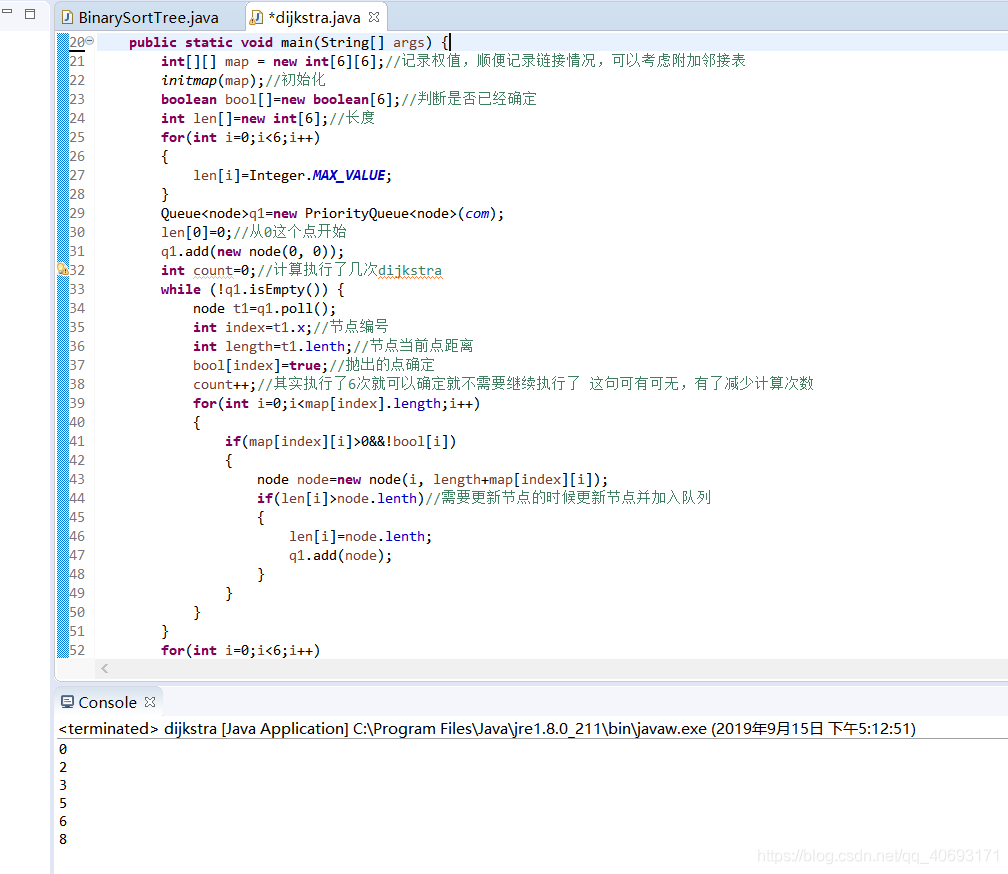
当然,dijkstra算法比较灵活,实现方式也可能有点区别,但是思想是不变的:一个贪心思路。dijkstra执行一次就能够确定一个点,所以只需要执行点的总和次数即可完成整个算法。
欢迎感谢小伙伴点赞、关注,赠人玫瑰,手有余香!蟹蟹!




