如果其他数都出现了 k 次,一个数出现了一次。那么如果 k 是偶数,还是把所有的数异或起来就行了。如果 k 是奇数,那么统计每一位是 1 的个数,然后模 k 取余数就能得到那个单独的数了 。其中有sum = kn + 1
位运算的解法是有限状态机+位运算,感觉有点难理解,自己推敲一遍勉强可以理解,自己画一个状态表,然后推导出响应的公式就比较好了。
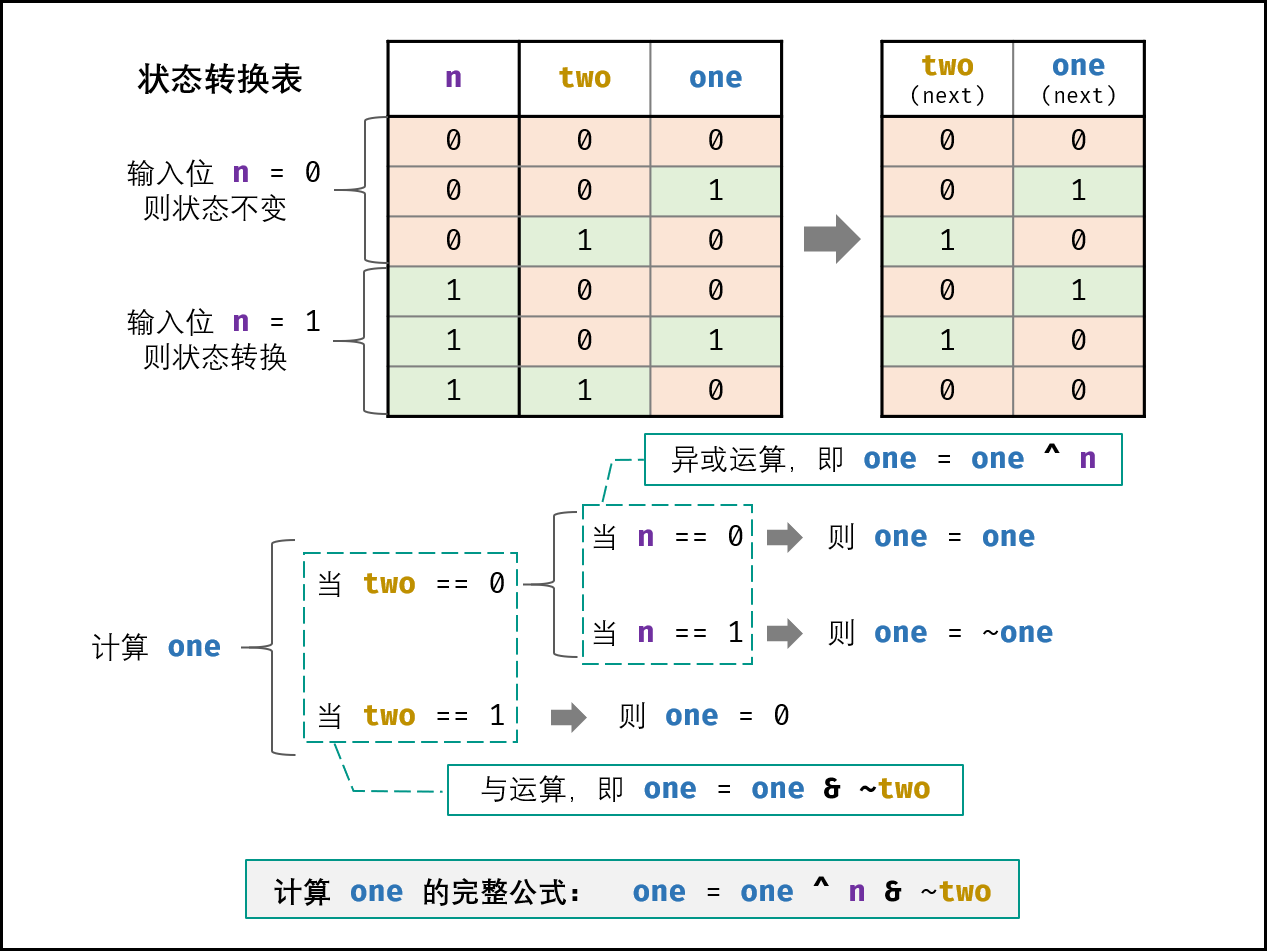
我是先看题解1, 在看题解2,才搞明白了。
【自动机+位运算】最详细的推导过程
图片来源:有限状态自动机 + 位运算,清晰图解-此题解清晰
几乎每道题都能看到题解2的作者,佩服不已,时而习之,但求甚解。
class Solution: def singleNumber(self, nums: List[int]) -> int: ones, twos = 0, 0 for num in nums: ones = ones ^ num & ~twos twos = twos ^ num & ~ones return ones LeetCode-260. 只出现一次的数字 III给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。
输入: [1,2,1,3,2,5] 输出: [3,5]注意:
结果输出的顺序并不重要,对于上面的例子, [5, 3] 也是正确答案。
你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
根据前面找一个不同数的思路算法,在这里把所有元素都异或,那么得到的结果就是那两个只出现一次的元素异或的结果。
如果我们把原数组分成两组,只出现过一次的两个数字分别在两组里边,那么问题就转换成之前的老问题了,只需要这两组里的数字各自异或,答案就出来了。
那么通过什么把数组分成两组呢?
放眼到二进制,我们要找的这两个数字是不同的,所以它俩至少有一位是不同的,所以我们可以根据这一位,把数组分成这一位都是 1 的一类和这一位都是 0 的一类,这样就把这两个数分到两组里了。
那么怎么知道那两个数字哪一位不同呢?
回到我们异或的结果,如果把数组中的所有数字异或,最后异或的结果,其实就是我们要找的两个数字的异或。而异或结果如果某一位是 1,也就意味着当前位两个数字一个是 1 ,一个是 0,也就找到了不同的一位。
以上思路源于作者:windliang
class Solution: def FindNumsAppearOnce(self, nums): length = len(nums) if length <= 0: return nums result = 0 # 先将所有数子异或得到一个值 for num in nums: result ^= num # 找到这个值最低位二进制位1的位置,根据这个位置来区分两个数组,分别异或求出只出现一次的数字 firstBitIndex = self.FindFirstBit(result) n1, n2 = 0, 0 for num in nums: if self.IsSameBit(num, firstBitIndex): n1 ^= num else: n2 ^= num return n1, n2 def FindFirstBit(self, num): indexBit = 0 while num & 1 == 0: indexBit += 1 num = num >> 1 return indexBit def IsSameBit(self, num, indexBit): num = num >> indexBit return num & 1 # 解放2 class Solution2: def FindNumsAppearOnce(self, nums): length = len(nums) if length <= 0: return [] diff = 0 for i in nums: diff ^= i n1, n2 = 0, 0 minDiff = self.getMinDiff(diff) for num in nums: if minDiff & num == 0: n1 ^= num n2 = diff ^ n1 return n1, n2 def getMinDiff(self, num): # 保留一个低位是1的数字 # 取负号其实就是先取反,再加 1,需要 补码 的知识。最后再和原数相与就会保留最低位的 1。比如 1010,先取反是 0101,再加 1,就是 0110,再和 1010 相与,就是 0010 了 return num & (-num) 如何得到二进制位只有一个1的数,几种方法diff &= -diff ; 这里 的做法。

