在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
平衡因子:某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子
AVL树的特点:
本身首先是一棵二叉搜索树。
带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)
为什么需要平衡树?
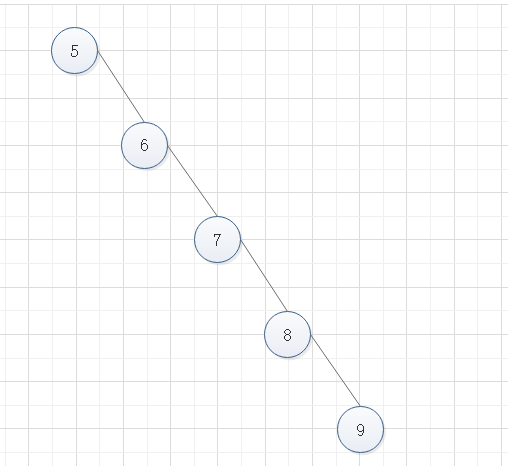
举个极端的例子:当我们将一个数组 [5, 6, 7, 8, 9]转换成二叉排序树时,它的二叉树图会如下图所示。
可以看出这时二叉树趋近于链表,虽然它的插入和删除的效率不会受到影响,但是查找的效率就有所降低了,因为它和链表一样需要从头到尾查找。
AVL树的旋转操作有三种:
当右子树的高度高于左子树一层以上时进行的左旋转
当左子树的高度高于右子树一层以上时进行的右旋转
以及特殊情况下进行的双向旋转。
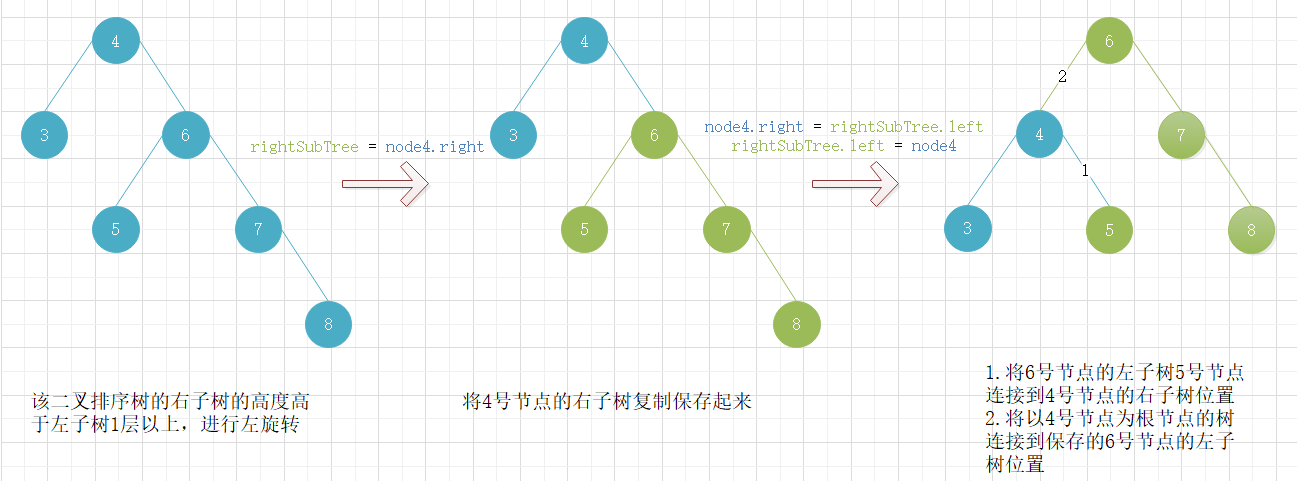
左旋转当二叉排序树的某一节点的右子树的高度高于左子树一层以上时,为了平衡二叉树排序树,需要对二叉排序树进行左旋转操作。
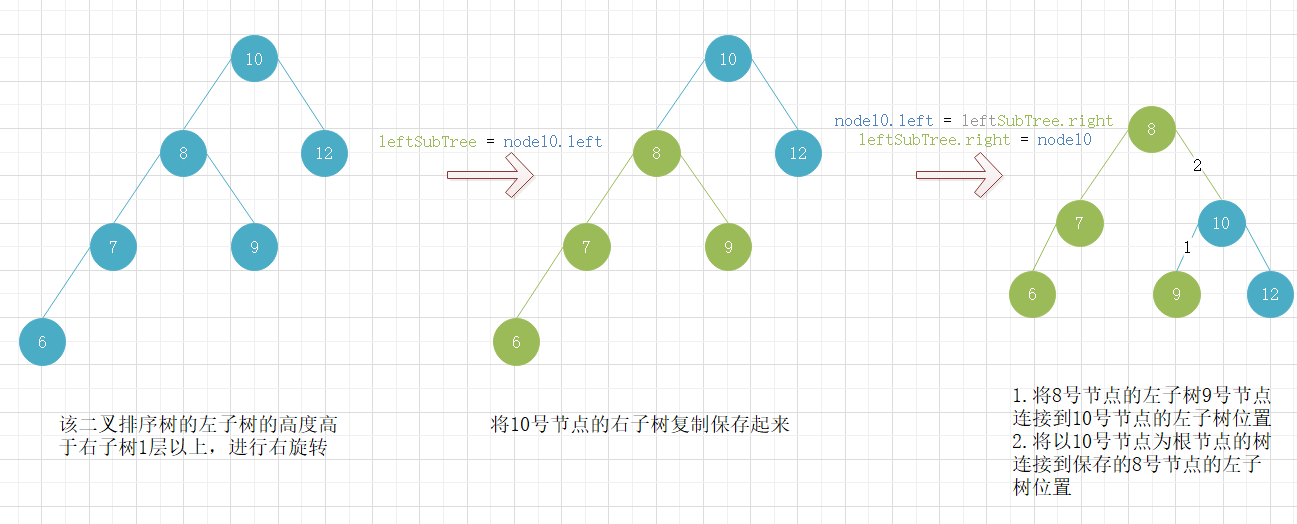
当二叉排序树的某一节点的左子树的高度高于右子树一层以上时,为了平衡二叉树排序树,需要对二叉排序树进行右旋转操作。
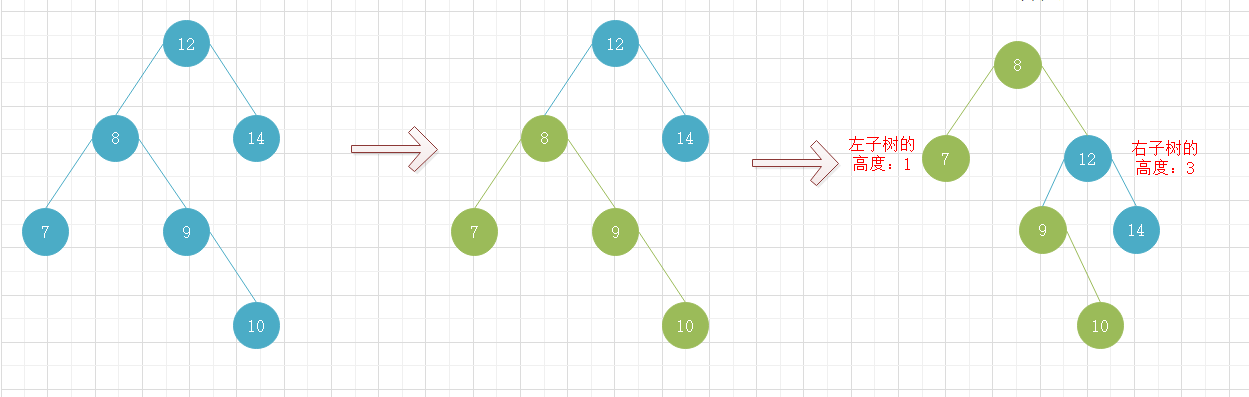
在进行左旋转或右旋转时需要判断一个特殊情况。如下图所示,根节点的左子树高度高于右子树一层以上,即平衡因子大于1,随即对该二叉树排序树进行右旋转操作,可以 看出右旋转后根节点右子树的高度高于左子树一层以上,平衡因子还是大于1,二叉排序树的平衡问题还是没解决。
观察该二叉排序树可以发现,根节点的左子节点8号节点的右子树的高度是高于左子树的,但只大于1,所以没有进入到旋转平衡操作,当我们为根节点下的子树进行右旋转时,会将8号节点较高的右子树连接到10号节点上,这时以10号节点为根节点的树高度就高于8号节点的左子树2层了,而随后我们又将该树来连接到8号节点的右子树上,就导致了旋转后平衡因子还是大于1的问题。
所以在遇到上面这种情况,即左旋转时右子树的左子树高于右子树的右子树或右旋转时左子树的右子树高于左子树的左子树,需先对较高的子树树进行一次右旋转或左旋转,再对整颗树进行左旋转或右旋转。
下图是当右旋转时左子树的右子树高于左子树的左子树的情况。
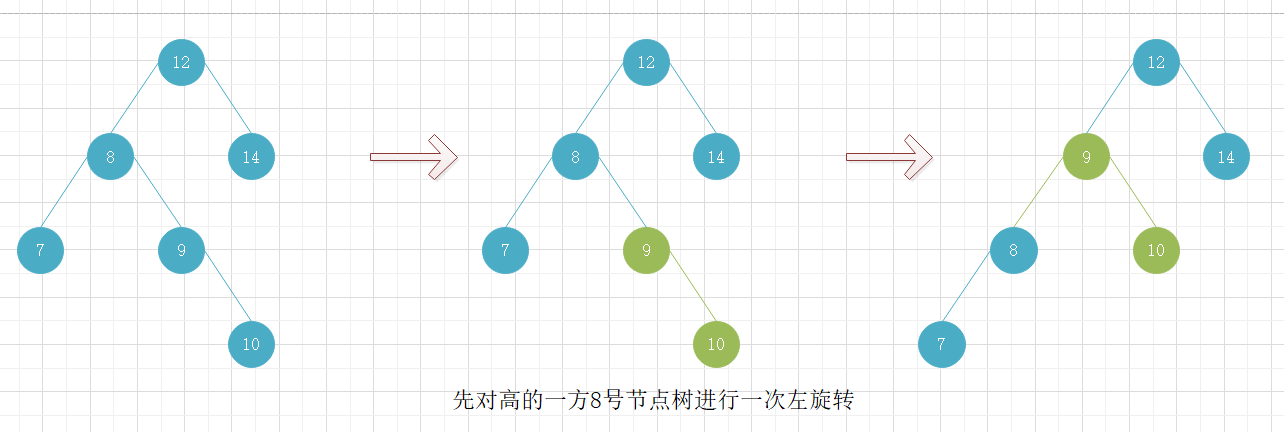
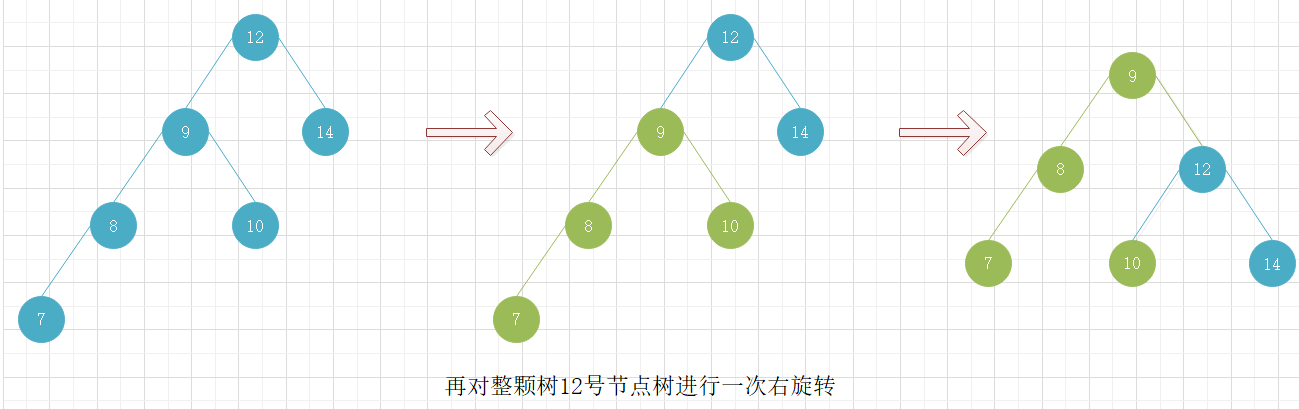
在进行旋转前,需要先判断以该节点为根节点的树是否需要进行旋转平衡,而判断是否需要旋转得知道该节点的左子树和右子树的高度。

