先提个问题,完全二叉树/满二叉树,区别?前者是指每一层都是紧凑靠左排列,最后一层可能未排满,后者是一种特殊的完全二叉树,
每层都是满的,即节点总数和深度满足N=(2^n) -1。堆Heap,一堆苹果,为了卖相好,越好看的越往上放,就是大顶堆;为了苹果堆
的稳定,质量越小越往上放,就是小顶堆;堆首先是完全二叉树,但只确保父节点和子节点大小逻辑,不关心左右子节点的大小关系,
通常是一个可以被看做一棵树的数组对象,是个很常见的结构,比如BST对象,都与堆有关系,今天就说下这个重要的数据结构和应用。
准备:
Idea2019.03/Gradle6.0.1/Maven3.6.3/JDK11.0.4
难度: 新手--战士--老兵--大师
目标:
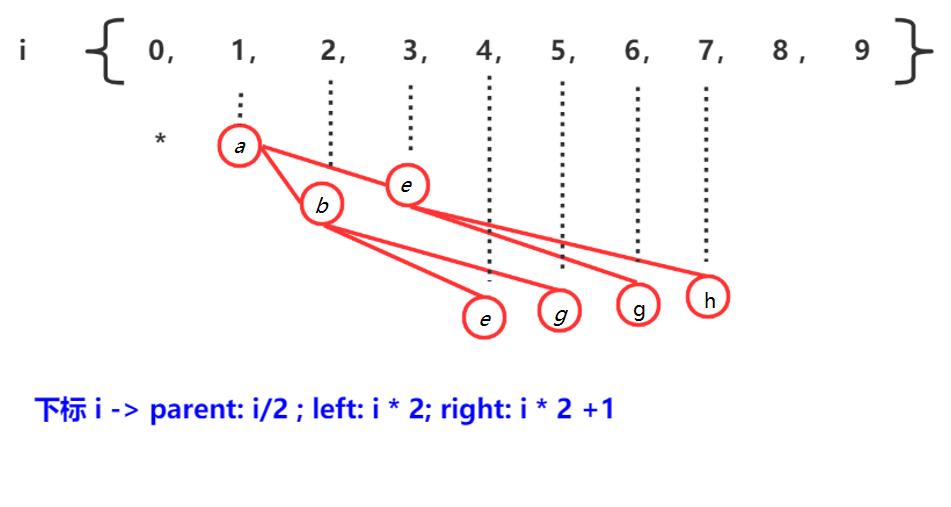
1 优先级队列为理解堆的原理,先看优先级队列,它是一种数据结构,插入或者删除元素的时候,元素会自动排序,(优先级不是狭义的数值大小,
但为了通俗理解,这里以字母序为例),通常使用数组存储,我们可以按照下图进行转换,序号 0 不用:
优先级队列的实现(Java版):
public class PriorityQueue<Key extends Character> { /** 存储元素的数组 */ private Key[] keys; private int N = 0; public PriorityQueue(int capacity){ // 下标0不用,多分配一个单位 keys = (Key[]) new Character[capacity + 1]; } public Key max(){ return keys[1]; } public void insert(Key e){ N ++; keys[N] = e; swim(N); } public Key delMax(){ Key max = keys[1]; swap(1,N); keys[N] = null; N --; // 让第一个元素下沉到合适的位置 sink(1); return max; } /** 上浮第k个元素*/ private void swim(int k){ // 比父节点小,即进行交换,直到根 while (k > 1 && less(parent(k),k)){ swap(k,parent(k)); k = parent(k); } } /** 下沉第 k 个元素*/ private void sink(int k){ while(k < N){ int small = left(k); if (right(k) < N && less(right(k),left(k))){ small = right(k); } if (less(k,small)){ swap(k,small); k = small; } } } private void swap(int i,int j){ Key temp = keys[i]; keys[i] = keys[j]; keys[j] = temp; } /** 元素i和j大小比较*/ private boolean less(int i,int j){ // 'a' - 'b' = -1 ; return keys[i].compareTo(keys[j]) > 0; } /** 元素i的父节点*/ private int parent(int i){ return i/2; } /** 元素i的左子节点*/ private int left(int i){ return i * 2; } /** 元素i的右子节点*/ private int right(int i){ return i * 2 + 1; } }

