初始条件和边界情况,动态规划一般是通过前一个节点来获取下一节点的值,所以我们需要明确其初始条件和数组dp的边界条件。就像数学归纳法,或是数列当中递推公式。
计算顺序,就是明确实现需求之前的上一个步骤要获得什么
读到这里,可能会有点糊涂,没事,下面会用示例来具体解释:
示例1:有三种硬币,面值分别是2元、3元、7元,则27元最少能用多少枚硬币组成
确定状态(最后一步、化为子问题):我们知道,题目需要的是最少能用多少枚硬币组成,我们需要定义一个长度为27的数组dp,而dp[i]就代表了对应总额所需要的最少硬币数目。我们假设最后一枚硬币面值为
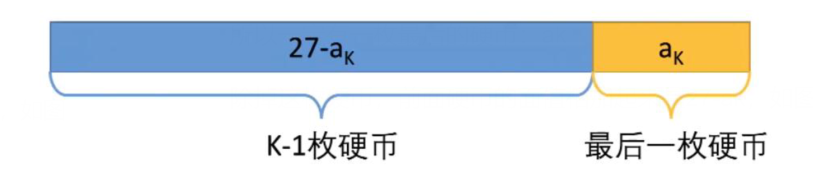
转移方程:通过如上分析,我们可以得到如下递推公式(转移方程),代表的意思就是除去最后一枚硬币的面值总额所需要的最少硬币数 + 1

