【LeetCode题解】142_环形链表2（Linked-List-Cycle-II）

@

描述

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

说明：不允许修改给定的链表。

进阶：
你是否可以不用额外空间解决此题？

解法一：哈希表 思路

最直接的解法就是利用一个集合保存每次遍历的节点的引用。之后，从链表头开始遍历，每遍历一个节点，就判断该节点的引用是否在集合中，如果不在集合中，则将该节点的引用放入集合中；如果在集合中，则返回该节点的引用（环的入口）。当然，如果能遍历到链表尾部，此时链表无环，返回 null。

Java 实现 /** * Definition for singly-linked list. * class ListNode { * int val; * ListNode next; * ListNode(int x) { * val = x; * next = null; * } * } */ import java.util.Set; import java.util.HashSet; public class Solution { public ListNode detectCycle(ListNode head) { ListNode curr = head; Set<ListNode> nodesSeen = new HashSet<>(); while (curr != null) { if (nodesSeen.contains(curr)) { return curr; } nodesSeen.add(curr); curr = curr.next; } return curr; } } Python 实现 # Definition for singly-linked list. # class ListNode(object): # def __init__(self, x): # self.val = x # self.next = None class Solution(object): def detectCycle(self, head): """ :type head: ListNode :rtype: ListNode """ curr = head nodes_seen = set() while curr: if curr in nodes_seen: return curr nodes_seen.add(curr) curr = curr.next return curr 复杂度分析

时间复杂度：\(O(n)\)

空间复杂度：\(O(n)\)

解法二：双指针 思路

和 LeetCode 第 141 题一样，如果不想占用额外的空间的话，可以采用双指针的方式。

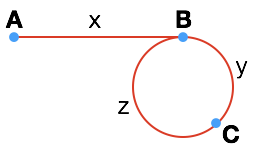
假设链表的起始节点为 A，环的入口节点为 B，两个指针（快慢指针）相交节点为 C，AB 两点之间的长度为 \(x\)，BC 两点之间的长度为 \(y\)，CB 两点之间的长度为 \(z\)。慢指针 slow 走过的长度为 \(x+y\)，快指针 fast 为了“赶上”慢指针，应该走过的长度为 \(x + y + z + y\)，同时，由于快指针的速度是慢指针的两倍，因此相同时间内，快指针走过的路程应该是慢指针（走过的路程）的两倍，即

\[ x + y + z + y = 2 (x + y) \]
化简得，
\[ x = z \]
因此，如果此时有另外一个慢指针 slow2 从起始节点 A 出发，则两个慢指针会在节点 B （环的入口）相遇。

Java 实现 /** * Definition for singly-linked list. * class ListNode { * int val; * ListNode next; * ListNode(int x) { * val = x; * next = null; * } * } */ public class Solution { public ListNode detectCycle(ListNode head) { ListNode slow = head, fast = head; while (fast != null && fast.next != null) { slow = slow.next; fast = fast.next.next; if (slow == fast) { ListNode slow2 = head; while (slow != slow2) { slow = slow.next; slow2 = slow2.next; } return slow; } } return null; } } // Runtime: 1 ms // Your runtime beats 100.00 % of python submissions. Python 实现 # Definition for singly-linked list. # class ListNode(object): # def __init__(self, x): # self.val = x # self.next = None class Solution(object): def detectCycle(self, head): """ :type head: ListNode :rtype: ListNode """ slow, fast = head, head while fast and fast.next: slow = slow.next fast = fast.next.next if slow == fast: slow2 = head while slow != slow2: slow = slow.next slow2 = slow2.next return slow return None # Runtime: 44 ms # Your runtime beats 99.73 % of python submissions. 复杂度分析

时间复杂度：\(O(n)\)，其中 \(n\) 表示链表的长度。最坏的情况下（链表有环），需要迭代的次数为 \(x + y + z = n\) 次，因此时间复杂度为 \(O(n)\)

空间复杂度：\(O(1)\)，只需要存储 3 个引用