当然真实的计算机原理差不多是这样的,不过会更复杂,比如不会像我们的加法器,一个一个的进位加,而是会先行进位,而且也不会用继电器,而是晶体管等等。
减法怎么弄?加法器我们搞出来了,那减法怎么做?减法需要有借位操作。
我们先拿熟悉的十进制来说。假设你的账户上限是499,你的透支额度是500,也就是说你的账户金额范围是 -500~499 这 1000 个数字,要求不能用负号来表示。
可以看到这是个三位数,而最大值就到 499 过,说明 500~999 之间的数没用,那拿来表示负数不就刚刚好吗?
所以让 500 表示 - 500 ,501 表示 -499,以此类推。
500,501.......998,999,000,001......498,499,让5、6、7、8、9开头的数都代表负数,而且是不是看起来还形成了个环形, 499 + 1 就变成 500 了,然后 999 + 1 变成 1000 ,但是只能三位数表示,所以溢出了变成 000。
这种处理叫 10 的补数,如果要把三位负数转为 10 的补数,就是让 999 减去它再加一,也就是说 10 的补数等于 9 的补数加一。
补数的概念:拿 9 的补数来说,将一个数从一串 9 中减去得到的结果就叫这个数 9 的补数,比如 123 ,它是三位数 ,999-123 = 876 所以 123 的 9 的补数就是 876,如果把结果 + 1那就是 10 的补数了。
就拿 -499 来说,我们要转化成补数,就是 999 - 499 + 1 等于 501 ,看上面的排列确实用 501 来代表 - 499。
那减去一个数不就是加上一个数的负数吗?所以通过补数我们就不需要做减法,只需要转成补数再相加就行了!
现在我们再换成二进制,二进制相比于十进制就更简单了。
拿八位二进制数来说,范围是 00000000~11111111, 对应的十进制是 0~255,但现在我们想让它能表示负数,前面十进制的时候我们将 5、6、7、8、9开头的正数来表示负数,对应于二进制我们可以将第一位以1开头的作为负数。
那此时的范围就是:

如果你理解了上面的十进制转化,这个二进制肯定是没问题的,这其实就是算出 2 的补数,而 2 的补数又是 1 的补数 +1。
我们拿 125 来举个例子,125 二进制表示是 01111101,求 1 的补数就是 11111111 - 01111101,这个减法在二进制中不需要,因为这其实就是求反,还记得上文提到的反向器吗?
取反了之后再加一,就得到 2 的补码。
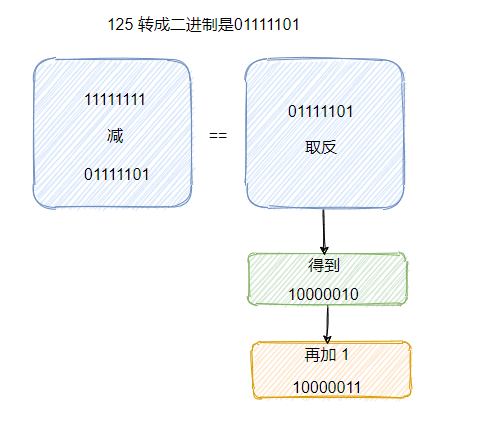
所以 -125 就是 10000011。
当然这一切的前提都是数字的位数需要固定,所以计算机中的位数就是固定的,超出了就会溢出,到这里你应该可以理解计算机中的补码是怎么来的,而且理解了为什么最大值 +1会变成最小值?
所以减法我们只需要改造一下上面的加法器,给个开关表示要这个数是负数,如果是负数则进行一波反向器操作然后再 +1,之后再进行加法操作即可得到最终的结果。
乘法和除法我就不分析了,一样也能通过加减法来实现。
振荡器(时钟)、锁存器(触发器)和计数器当然这个和我们所认识的计算机还差很多,现在只能进行一些非常简陋的加减操作,别急我们先来看看这个电路。
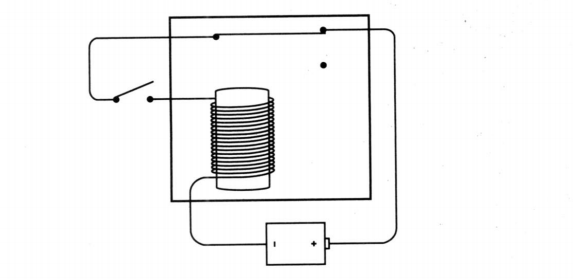
这个电路很有意思,当你闭合开关的时候电路通了,此时由于电磁效应可动棒被吸了下来,电路就断了,断了之后磁性消失了可动棒又移了上去,这样电路又通了,如此往复。
这种电路叫振荡器,这是一个很关键的东西,记住它。
它的来回振荡其实就是在输出 0 和 1 的交替序列,画成图如下所示:
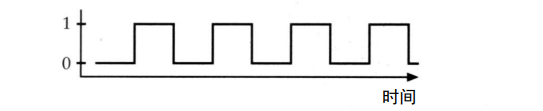
随着时间的变化在 0 和 1之间交替变化,因此也称之为时钟。

