希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
算法步骤我们来看下希尔排序的基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2, (n/2)/2, ..., 1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
选择一个增量序列{t1, t2, …, tk},其中(ti>tj, i<j, tk=1);
按增量序列个数k,对序列进行k趟排序;
每趟排序,根据对应的增量t,将待排序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。仅增量因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度。
图解算法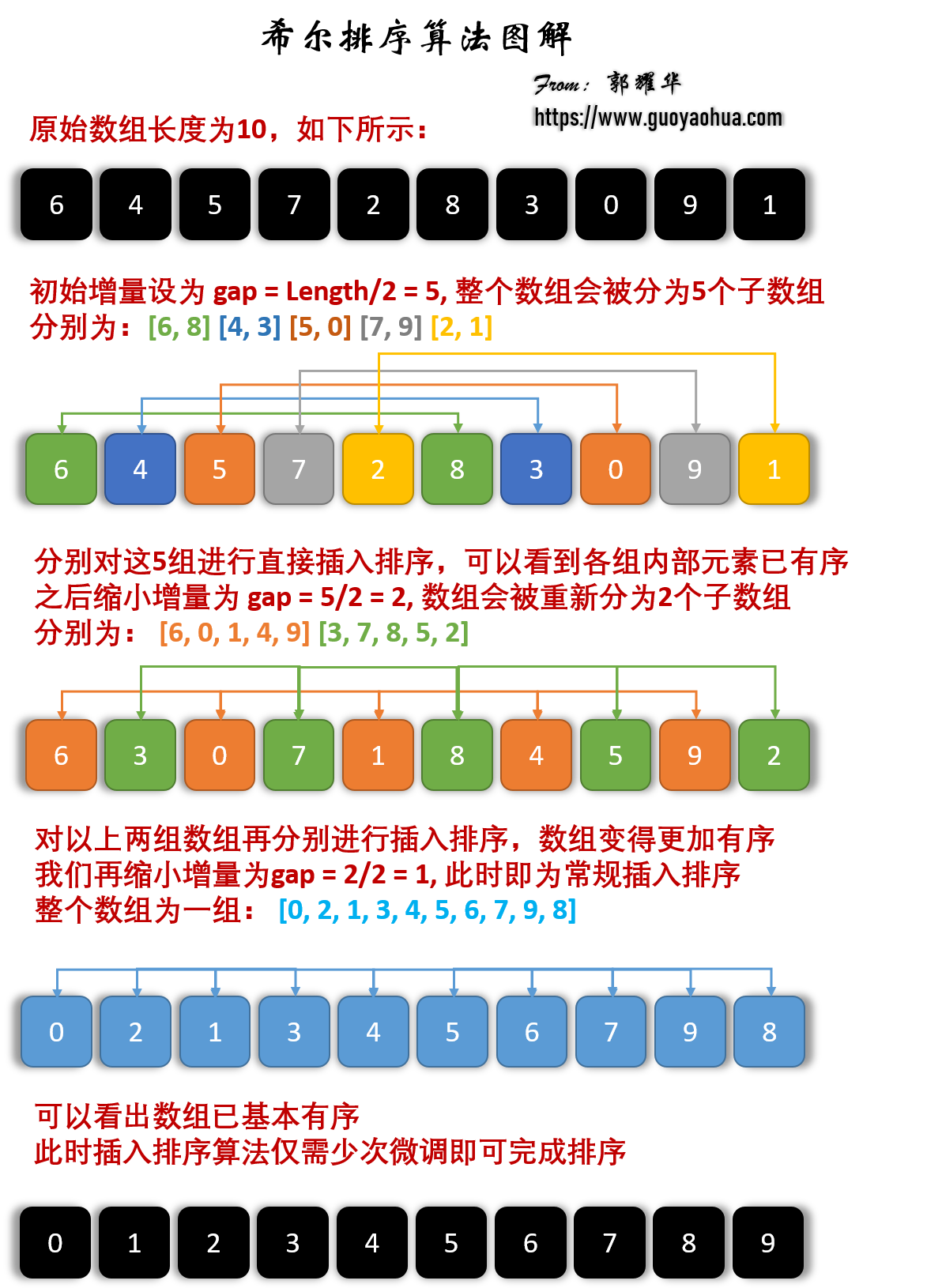
JAVA
/** * 希尔排序 * * @param arr * @return arr */ public static int[] ShellSort(int[] arr) { int n = arr.length; int gap = n / 2; while (gap > 0) { for (int i = gap; i < n; i++) { int current = arr[i]; int preIndex = i - gap; // Insertion sort while (preIndex >= 0 && arr[preIndex] > current) { arr[preIndex + gap] = arr[preIndex]; preIndex -= gap; } arr[preIndex + gap] = current; } gap /= 2; } return arr; }Python
def ShellSort(arr): n = len(arr) # 初始步长 gap = n // 2 while gap > 0: for i in range(gap, n): # 根据步长进行插入排序 current = arr[i] preIndex = i - gap # 插入排序 while preIndex >= 0 and arr[preIndex] > current: arr[preIndex+gap] = arr[preIndex] preIndex -= gap arr[preIndex+gap] = current # 得到新的步长 gap = gap // 2 return arr 归并排序(Merge Sort)归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间。
算法步骤归并排序算法是一个递归过程,边界条件为当输入序列仅有一个元素时,直接返回,具体过程如下:
如果输入内只有一个元素,则直接返回,否则将长度为n的输入序列分成两个长度为n/2的子序列;
分别对这两个子序列进行归并排序,使子序列变为有序状态;
设定两个指针,分别指向两个已经排序子序列的起始位置;
比较两个指针所指向的元素,选择相对小的元素放入到合并空间(用于存放排序结果),并移动指针到下一位置;
重复步骤3 ~4直到某一指针达到序列尾;
将另一序列剩下的所有元素直接复制到合并序列尾。
图解算法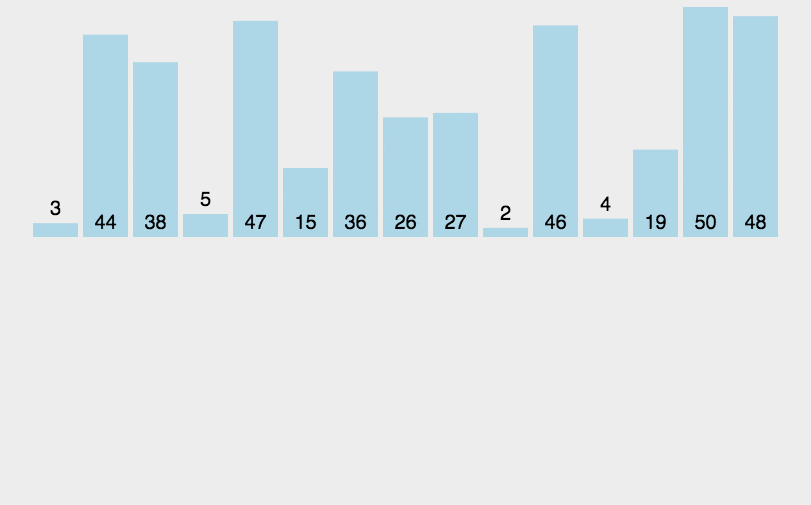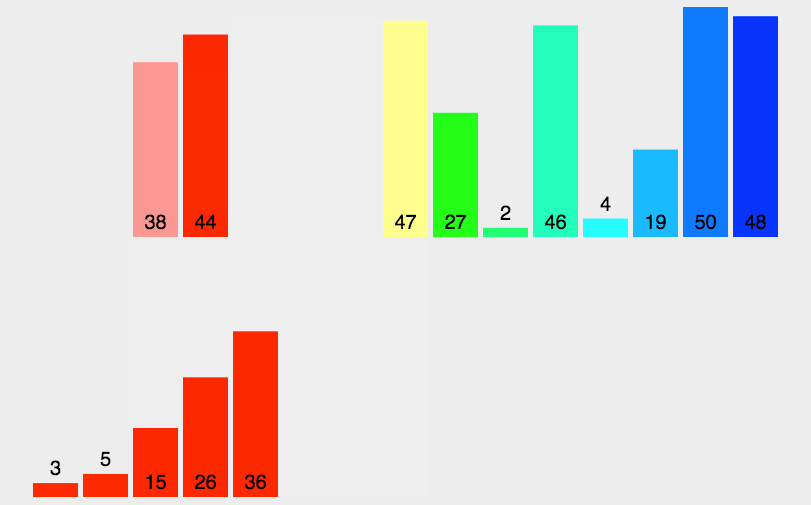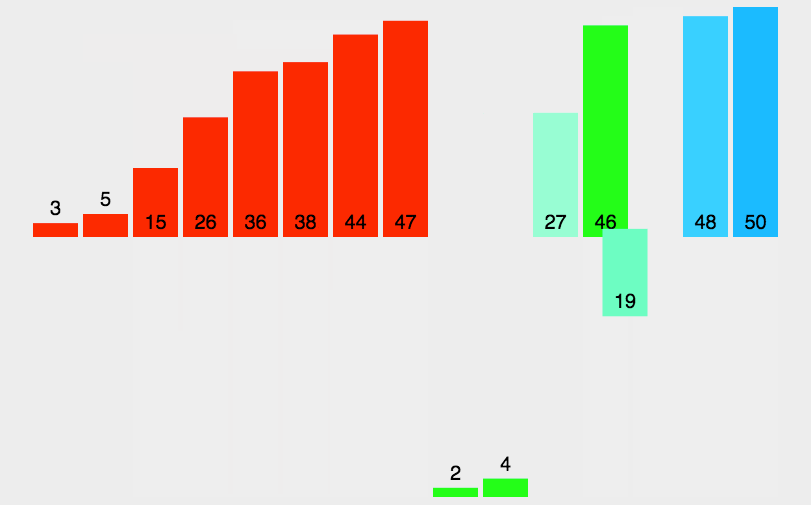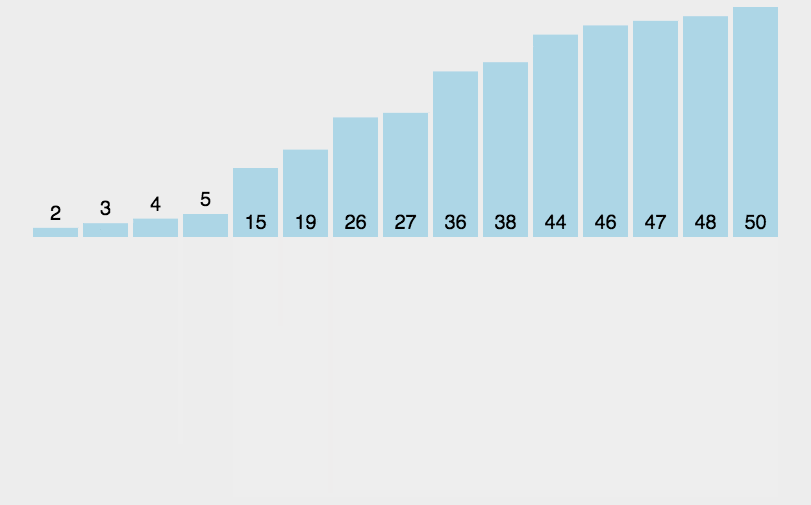
JAVA
/** * 归并排序 * * @param arr * @return arr */ public static int[] MergeSort(int[] arr) { if (arr.length <= 1) { return arr; } int middle = arr.length / 2; int[] arr_1 = Arrays.copyOfRange(arr, 0, middle); int[] arr_2 = Arrays.copyOfRange(arr, middle, arr.length); return Merge(MergeSort(arr_1), MergeSort(arr_2)); } /** * Merge two sorted arrays * * @param arr_1 * @param arr_2 * @return sorted_arr */ public static int[] Merge(int[] arr_1, int[] arr_2) { int[] sorted_arr = new int[arr_1.length + arr_2.length]; int idx = 0, idx_1 = 0, idx_2 = 0; while (idx_1 < arr_1.length && idx_2 < arr_2.length) { if (arr_1[idx_1] < arr_2[idx_2]) { sorted_arr[idx] = arr_1[idx_1]; idx_1 += 1; } else { sorted_arr[idx] = arr_2[idx_2]; idx_2 += 1; } idx += 1; } if (idx_1 < arr_1.length) { while (idx_1 < arr_1.length) { sorted_arr[idx] = arr_1[idx_1]; idx_1 += 1; idx += 1; } } else { while (idx_2 < arr_2.length) { sorted_arr[idx] = arr_2[idx_2]; idx_2 += 1; idx += 1; } } return sorted_arr; }Python
def Merge(arr_1, arr_2): sorted_arr = [] idx_1 = 0 idx_2 = 0 while idx_1 < len(arr_1) and idx_2 < len(arr_2): if arr_1[idx_1] < arr_2[idx_2]: sorted_arr.append(arr_1[idx_1]) idx_1 += 1 else: sorted_arr.append(arr_2[idx_2]) idx_2 += 1 if idx_1 < len(arr_1): while idx_1 < len(arr_1): sorted_arr.append(arr_1[idx_1]) idx_1 += 1 else: while idx_2 < len(arr_2): sorted_arr.append(arr_2[idx_2]) idx_2 += 1 return sorted_arr def MergeSort(arr): if len(arr) <= 1: return arr mid = int(len(arr)/2) arr_1, arr_2 = arr[:mid], arr[mid:] return Merge(MergeSort(arr_1), MergeSort(arr_2)) 算法分析稳定性:稳定
时间复杂度:最佳:O(nlogn) 最差:O(nlogn) 平均:O(nlogn)
空间复杂度:O(n)
快速排序(Quick Sort)
