二叉树的遍历是在面试使比较常见的项目了。对于二叉树的前中后层序遍历,每种遍历都可以递归和循环两种实现方法,且每种遍历的递归实现都比循环实现要简洁。下面做一个小结。
一、中序遍历前中后序三种遍历方法对于左右结点的遍历顺序都是一样的(先左后右),唯一不同的就是根节点的出现位置。对于中序遍历来说,根结点的遍历位置在中间。
所以中序遍历的顺序:左中右
1.1 递归实现每次递归,只需要判断结点是不是None,否则按照左中右的顺序打印出结点value值。
class Solution: def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ if not root: return [] return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right) 1.2 循环实现循环比递归要复杂得多,因为你得在一个函数中遍历到所有结点。但是有句话很重要:
对于树的遍历,循环操作基本上要用到栈(stack)这个结构
对于中序遍历的循环实现,每次将当前结点(curr)的左子结点push到栈中,直到当前结点(curr)为None。这时,pop出栈顶的第一个元素,设其为当前结点,并输出该结点的value值,且开始遍历该结点的右子树。
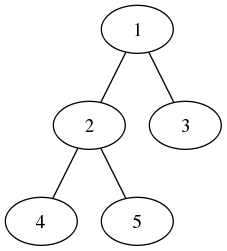
例如,对于上图的一个二叉树,其循环遍历过程如下表:
No. 输出列表sol 栈stack 当前结点curr1 [] [] 1
2 [] [1] 2
3 [] [1,2] 4
4 [] [1,2,4] None
5 [4] [1,2] 4 -> None(4的右结点)
6 [4,2] [1] 2 -> 5
7 [4,2] [1,5] None(5的左结点)
8 [4,2,5] [1] 5 -> None(5的右结点)
9 [4,2,5,1] [] 3
10 [4,2,5,1] [3] None
11 [4,2,5,1,3] [] None
可见,规律为:当前结点curr不为None时,每一次循环将当前结点curr入栈;当前结点curr为None时,则出栈一个结点,且打印出栈结点的value值。整个循环在stack和curr皆为None的时候结束。
class Solution: def inorderTraversal(self, root): stack = [] sol = [] curr = root while stack or curr: if curr: stack.append(curr) curr = curr.left else: curr = stack.pop() sol.append(curr.val) curr = curr.right return sol 二、前序遍历和后序遍历按照上面的说法,前序遍历指根结点在最前面输出,所以前序遍历的顺序是:中左右
后序遍历指根结点在最后面输出,所以后序遍历的顺序是:左右中
2.1 递归实现递归实现与中序遍历几乎完全一样,改变一下打印的顺序即可:
class Solution: def preorderTraversal(self, root): ##前序遍历 """ :type root: TreeNode :rtype: List[int] """ if not root: return [] return [root.val] + self.inorderTraversal(root.left) + self.inorderTraversal(root.right) def postorderTraversal(self, root): ##后序遍历 """ :type root: TreeNode :rtype: List[int] """ if not root: return [] return self.inorderTraversal(root.left) + self.inorderTraversal(root.right) + [root.val]改动的地方只有return时函数的打印顺序。
2.2 循环实现为什么把前序遍历和后序遍历放在一起呢?Leetcode上前序遍历是medium难度,后序遍历可是hard难度呢!
实际上,后序遍历不就是前序遍历的“反过程”嘛!
先看前序遍历。我们仍然使用栈stack,由于前序遍历的顺序是中左右,所以我们每次先打印当前结点curr,并将右子结点push到栈中,然后将左子结点设为当前结点。入栈和出栈条件(当前结点curr不为None时,每一次循环将当前结点curr入栈;当前结点curr为None时,则出栈一个结点)以及循环结束条件(整个循环在stack和curr皆为None的时候结束)与中序遍历一模一样。

