插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
(每步将一个待排序的元素,按其排序码大小插入到前面已经排好序的一组元素的适当位置上去,直到元素全部插入为止)
(图片来源:https://www.cnblogs.com/fivestudy/p/10212306.html)
具体算法描述如下:
1、将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列;
2、取出下一个元素,在已经排序的元素序列中从后向前扫描;
3、如果该元素(已排序)大于新元素,将该元素移到下一位置;
4、重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
5、将新元素插入到该位置后;
6、重复步骤2~5。
排序过程示例如下图:
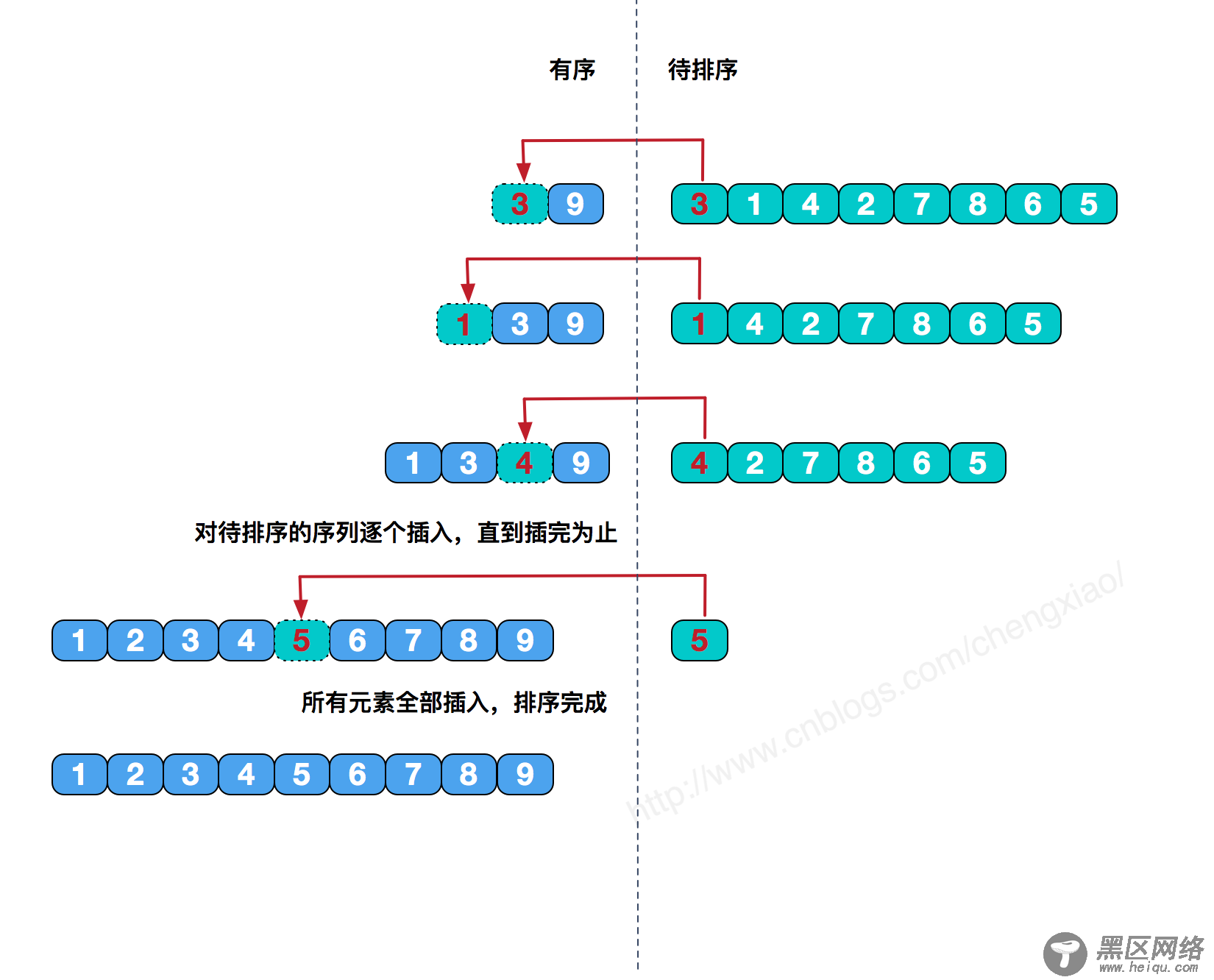
(图片来源:https://www.cnblogs.com/chengxiao/p/6103002.html)
代码实现:
/* 插入排序*/
int num[5] = {3, 7, 1, 8, 5};
int pos, cur;
int i;
int length = sizeof(num)/sizeof(num[0]);
for (i = 1; i < length; i++)
{
pos = i -1 ; //有序序列的最后一个元素位置
cur = num[i]; //保存待排序元素的值
while ( pos >= 0 && num[pos] > cur)
{
num[pos + 1] = num[pos];
pos--;
}
num[pos + 1] = cur; //将待排序元素插入数组中
}
也可以写成两个for循环的形式,效果相同
/* 插入排序*/
int num[5] = {3, 7, 1, 8, 5};
int cur;
int i, j;
int length = sizeof(num)/sizeof(num[0]);
for (i = 1; i < length; i++)
{
cur = num[i]; //待排序元素
for (j = i - 1; j >= 0 && num[j] > cur; j--)
{
num[j + 1] = num[j];
}
num[j + 1] = cur;
}
排序过程:以上面的例子来说排序的对象是 3,7,1,8,5 数组长度为5,因为第一个元素可以认为已经被排序,所以for循环的次数是:5(数组长度) - 1 = 4
第一次for循环:
3>7不成立,插入待排序元素,数组不变,此时有序序列为3,7
第二次for循环:
7>1成立,数组变成3,7,7,8,5
3>1成立,数组变成3,3,7,8,5
插入待排序元素,此时数组为1,3,7,8,5,有序序列为1,3,7
第三次for循环:
7>8不成立,插入待排序元素,数组不变,此时有序序列为1,3,7,8
第四次for循环:
8>5成立,数组变成1,3,7,8,8
7>5成立,数组变成1,3,7,7,8
3>5不成立,插入待排序元素,此时数组为1,3,5,7,8,有序序列为1,3,5,7,8,排序完成


