本文首先最小生成树三种算法简单描述,再介绍Prim算法描述、算法正确性证明并给出例子,最后用C语言实现该算法,并给出测试结果。
一、最小生成树算法
现实中不少问题可以抽象成最小生成树模型,比如道路铺设,使得任何两个地方可达,并且使得总费用最省。最小生成树算法主要有:
(1) Kruskal(克鲁斯克尔)算法
从G中的最小边开始,进行避圈式扩张。从符合扩展边(新加入的边不会构成回路)选择权值最小的边进行扩展。
(2) 管梅谷的破圈法
不断破圈(从赋权图G的任意圈开始,去掉该圈中权值最大的一条边,称为破圈),直到G中没有圈为止,最后剩下的G的子图为G的最小生成树。
(3) Prim算法
对于连通赋权图G的任意一个顶点u,选择与点u关联的且权值最小的边作为最小生成树的第一条边e1。在接下来的边e2,e3,…,en-1 ,在与一条已经选取的边只有一个公共端点的的所有边中,选取权值最小的边。
二、Prim算法
(1) 算法描述
Prim算法利用贪心法思想,算法描述如下:
在图G=(V, E) (V表示顶点 ,E表示边)中,从集合V中任取一个顶点(例如取顶点v0)放入集合 U中,这时 U={v0},集合T(E)为空。
从v0出发寻找与U中顶点相邻(另一顶点在V中)权值最小的边的另一顶点v1,并使v1加入U。即U={v0,v1 },同时将该边加入集合T(E)中。
重复(2),直到U = V为止。
这时T(E)中有n-1条边,T = (U, T(E))就是一棵最小生成树。
(2) 算法正确性证明
即证明用该算法得到的生成树是最小的。如下:
设prim生成的树为G0,假设存在Gmin使得cost(Gmin)<cost(G0),则在Gmin中存在(u,v)不属于G0,将(u,v)加入G0中可得一个环,且(u,v)不是该环的最长边,这与prim每次生成最短边矛盾。故假设不成立,命题得证[1]。
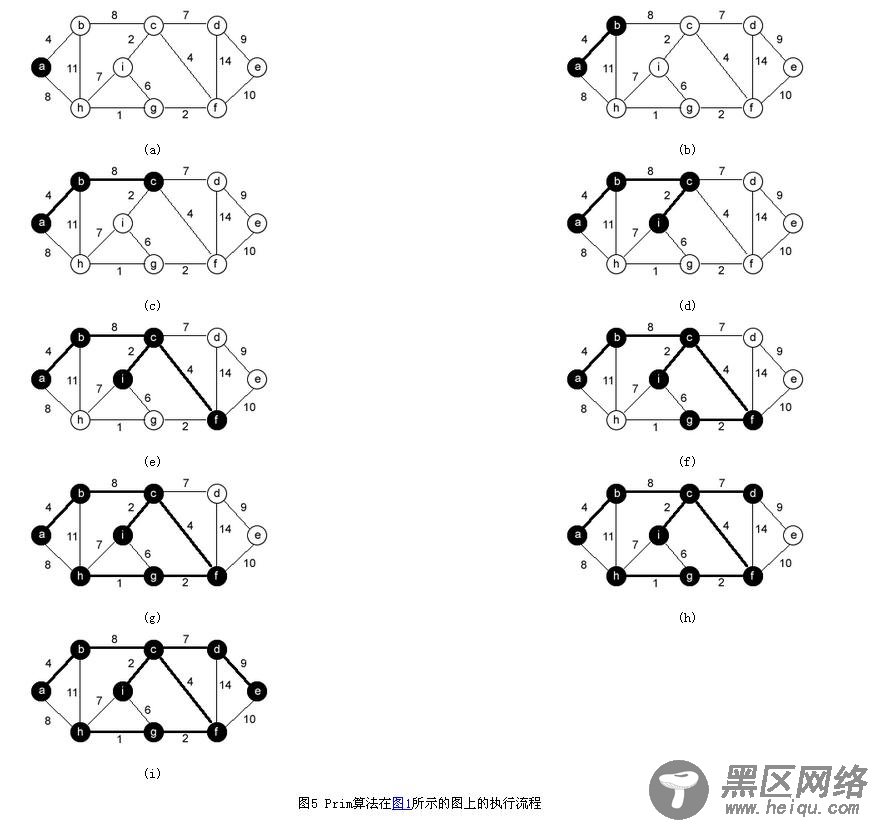
(3) 例子