
情况1: 当父节点为黑色时插入子节点 空树插入根节点,将根节点红色变为黑色 父节点为红色左节点,叔父节点为黑色,插入左子节点,那么通过【左左节点旋转】
情况2: - 父节点和叔父节点都为红色 父节点为红色左节点,叔父节点为黑色,插入右子节点,那么通过【左右节点旋转】
情况3: - - 父节点为红色右节点,叔父节点为黑色,插入左子节点,那么通过【右左节点旋转】
情况4: - - 父节点为红色右节点,叔父节点为黑色,插入右子节点,那么通过【右右节点旋转】
四. 红黑树节点删除
相比较于红黑树的节点插入,删除节点更为复杂,我们从子节点是否为null和红色为思考维度来讨论。
4.1 子节���至少有一个为null当待删除的节点的子节点至少有一个为null节点时,删除了该节点后,将其有值的节点取代当前节点即可,若都为null,则将当前节点设置为null,当然如果违反规则了,则按需调整,如【变色】以及【旋转】。
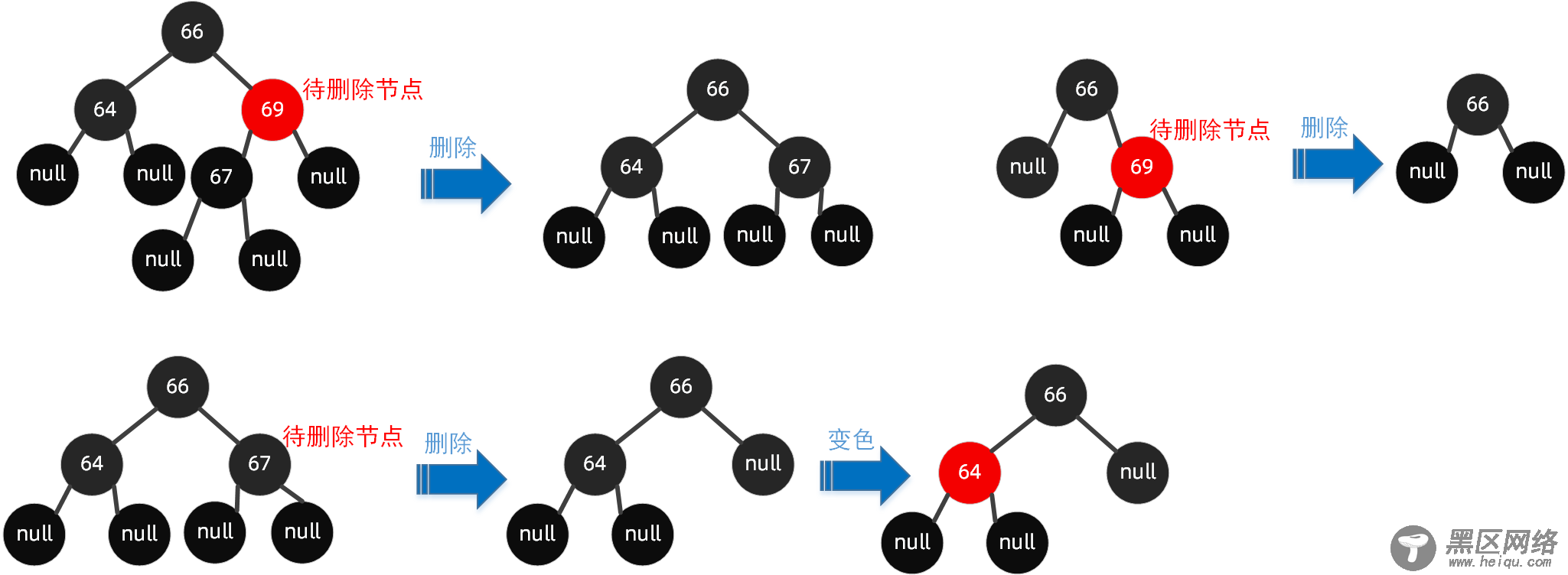
这种情况下,
第一步:找到该节点的前驱或者后继
前驱:左子树中值最大的节点(可得出其最多只有一个非null子节点,可能都为null);
后继:右子树中值最小的节点(可得出其最多只有一个非null子节点,可能都为null);
前驱和后继都是值最接近该节点值的节点,类似于该节点.prev = 前驱,该节点.next = 后继。
第二步:将前驱或者后继的值复制到该节点中,然后删掉前驱或者后继
如果删除的是左节点,则将前驱的值复制到该节点中,然后删除前驱;如果删除的是右节点,则将后继的值复制到该节点中,然后删除后继;
这相当于是一种“取巧”的方法,我们删除节点的目的是使该节点的值在红黑树上不存在,因此专注于该目的,我们并不关注删除节点时是否真是我们想删除的那个节点,同时我们也不需考虑树结构的变化,因为树的结构本身就会因为自动平衡机制而经常进行调整。
前面我们已经说了,我们要删除的实际上是前驱或者后继,因此我们就以前驱为主线来讲解,后继的学习可参考前驱,包括几种情况
4.2.1 前驱为黑色节点,并且有一个非null子节点
分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则4,因此需要进行自动平衡调整;
这里直接通过【变色】即可完成。
4.2.2 前驱为黑色节点,同时子节点都为null
分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则5,因此需要进行自动平衡调整;
这里直接通过【变色】即可完成。
4.2.3 前驱为红色节点,同时子节点都为null
分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,树的结构并没有打破规则。
4.3 红黑树删除总结红黑树删除的情况比较多,但也就存在以下情况:
删除的是根节点,则直接将根节点置为null;
待删除节点的左右子节点都为null,删除时将该节点置为null;
待删除节点的左右子节点有一个有值,则用有值的节点替换该节点即可;
待删除节点的左右子节点都不为null,则找前驱或者后继,将前驱或者后继的值复制到该节点中,然后删除前驱或者后继;

