分解:把数组A[p...r]分为A[p...q-1]与A[q+1...r]两部分,其中A[p...q-1]中的每个元素都小于等于A[q]而A[q+1...r]中的每个元素都大于等于A[q];
解决:通过递归调用快速排序,对子数组A[p...q-1]和A[q+1...r]进行排序;
合并:因为两个子数组是就地排序的,所以不需要额外的操作。
对于划分partition 每一轮迭代的开始,x=A[r], 对于任何数组下标k,有:
1) 如果p≤k≤i,则A[k]≤x。
2) 如果i+1≤k≤j-1,则A[k]>x。
3) 如果k=r,则A[k]=x。
代码如下:
#!/usr/bin/env python
# 快速排序
'''
划分 使满足 以A[r]为基准对数组进行一个划分,比A[r]小的放在左边,
比A[r]大的放在右边
快速排序的分治partition过程有两种方法,
一种是上面所述的两个指针索引一前一后逐步向后扫描的方法,
另一种方法是两个指针从首位向中间扫描的方法。
'''
#p,r 是数组A的下标
def partition1(A, p ,r):
'''
方法一,两个指针索引一前一后逐步向后扫描的方法
'''
x = A[r]
i = p-1
j = p
while j < r:
if A[j] < x:
i +=1
A[i], A[j] = A[j], A[i]
j += 1
A[i+1], A[r] = A[r], A[i+1]
return i+1
def partition2(A, p, r):
'''
两个指针从首尾向中间扫描的方法
'''
i = p
j = r
x = A[p]
while i < j :
while A[j] >= x and i < j:
j -=1
A[i] = A[j]
while A[i]<=x and i < j:
i +=1
A[j] = A[i]
A[i] = x
return i
# quick sort
def quick_sort(A, p, r):
'''
快速排序的最差时间复杂度为O(n2),平时时间复杂度为O(nlgn)
'''
if p < r:
q = partition2(A, p, r)
quick_sort(A, p, q-1)
quick_sort(A, q+1, r)
if __name__ == '__main__':
A = [5,-4,6,3,7,11,1,2]
print 'Before sort:',A
quick_sort(A, 0, 7)
print 'After sort:',A
不稳定,时间复杂度 最理想 O(nlogn)最差时间O(n^2)
说下python中的序列:
列表、元组和字符串都是序列,但是序列是什么,它们为什么如此特别呢?序列的两个主要特点是索引操作符和切片操作符。索引操作符让我们可以从序列中抓取一个特定项目。切片操作符让我们能够获取序列的一个切片,即一部分序列,如:a = ['aa','bb','cc'], print a[0] 为索引操作,print a[0:2]为切片操作。
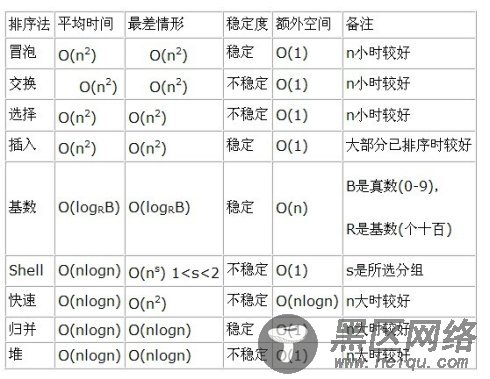
总结如下:
CentOS上源码安装Python3.4
《Python核心编程 第二版》.(Wesley J. Chun ).[高清PDF中文版]
《Python开发技术详解》.( 周伟,宗杰).[高清PDF扫描版+随书视频+代码]
Python脚本获取Linux系统信息
在Ubuntu下用Python搭建桌面算法交易研究环境

