Python教程之绘制Mandelbrot集合

一. 分形与混沌

 

自然界的很多事物，如树木、云彩、山脉、雪花、海岸线等，都呈现出传统几何学所不能描述的形状，这些形状都有如下的特性：

有着十分精细的不规则结构

整体与局部相似

分形与混沌的关系密切，多是以自组织系统为其研究对象，而含义又各不相同。自组织现象常常是时空有序的结构，是复杂的系统，用传统的简化方法无法解决。分形几何学就是用来研究这样一类几何形状的科学，混沌中有时包容着分形，而分形有时又孕育着混沌。分形更注重形态或几何特性、图形的描述；混沌更偏重数理的动力学及动力学与图形结合的多方位的描述和研究。分形更看重有自相似性的系统，而混沌涉及面似乎更广，对所有的有序与无序、有序与有序现象都感兴趣。

 

二. Mandelbrot集合

        Mandelbrot（曼德布洛特）集合是在复平面上组成分形的点的集合。Mandelbrot集合可以用下面的复二次多项式定义：

其中c是一个复数。对于每一个c，从z=0开始对函数进行迭代。序列的值或者延伸到无限大，或者只停留在有限半径的圆盘内。Mandelbrot集合就是使以上序列不发散的所有c点的集合。用程序绘制Mandelbrot集合时不能进行无限次迭代，最简单的方法是使用逃逸时间（迭代次数）进行绘制，具体算法如下：

判断每次调用函数得到的结果是否在半径R之内，即复数的模小于R

记录下模大于R时的迭代次数

迭代最多进行N次

不同的迭代次数的点使用不同的颜色绘制

三. Mandelbrot程序

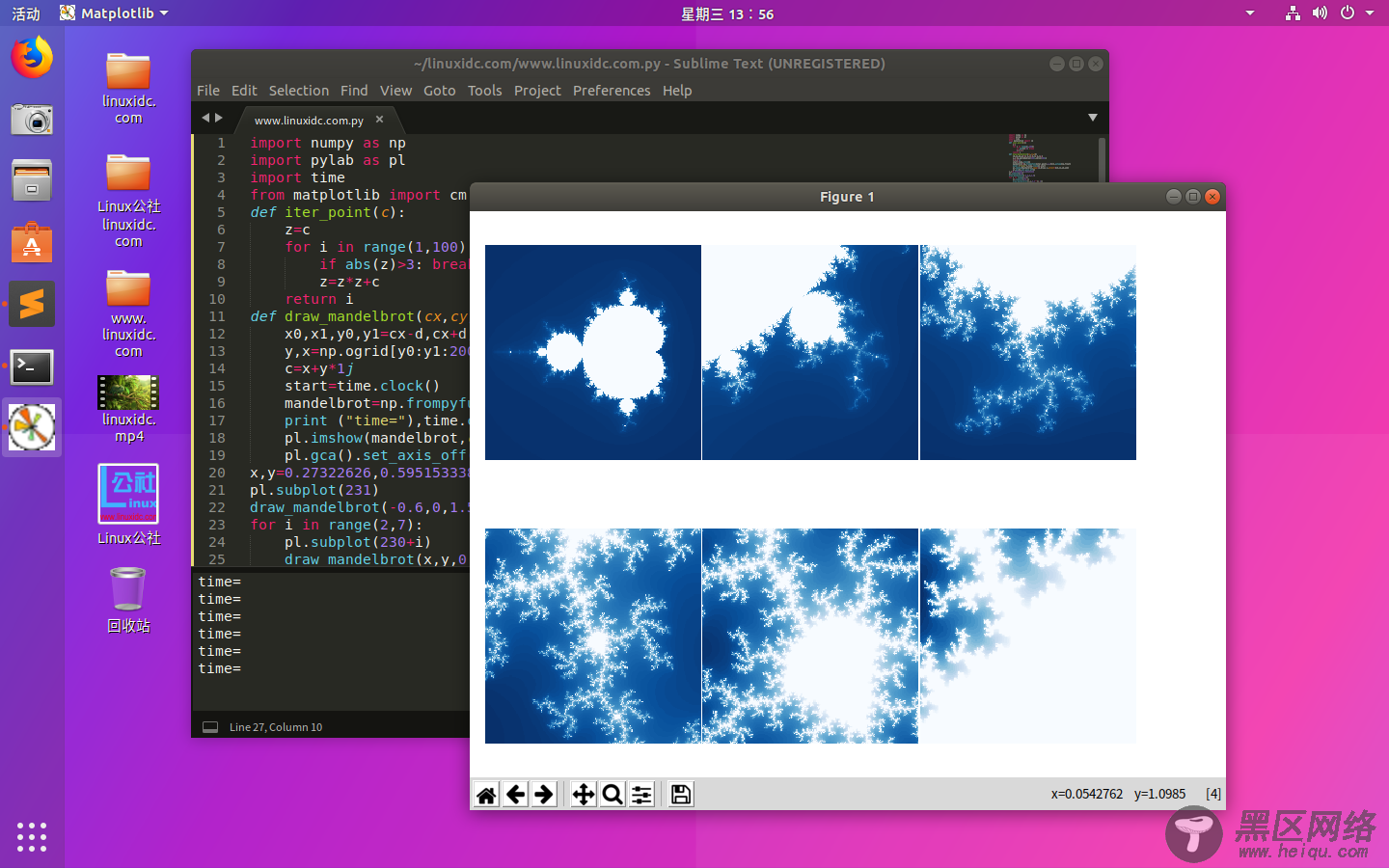
import numpy as np import pylab as pl import time from matplotlib import cm def iter_point(c): z=c for i in range(1,100): if abs(z)>3: break z=z*z+c return i def draw_mandelbrot(cx,cy,d): x0,x1,y0,y1=cx-d,cx+d,cy-d,cy+d y,x=np.ogrid[y0:y1:200j,x0:x1:200j] c=x+y*1j start=time.clock() mandelbrot=np.frompyfunc(iter_point,1,1)(c).astype(np.float) print ("time="),time.clock()-start pl.imshow(mandelbrot,cmap=cm.Blues_r,extent=[x0,x1,y0,y1]) pl.gca().set_axis_off() x,y=0.27322626,0.595153338 pl.subplot(231) draw_mandelbrot(-0.6,0,1.5) for i in range(2,7): pl.subplot(230+i) draw_mandelbrot(x,y,0.2**(i-1)) pl.subplots_adjust(0.02,0,0.88,1,0.01,0) pl.show()

运行效果如下图：