但要保持红黑树的性质,结点不能乱挪,还得靠变色了。怎么变?具体情景有不同变法,后面会具体讲到,现在只需要记住红黑树总是通过旋转和变色达到自平衡。
Balabala 了这么多,相信你对红黑树有一定印象了,那么现在来考考你。
思考题 1:黑结点可以同时包含一个红子结点和一个黑子结点吗? (答案见文末)
接下来先讲解红黑树的查找热热身。
红黑树查找
因为红黑树是一颗二叉平衡树,并且查找不会破坏树的平衡,所以查找跟二叉平衡树的查找无异:
从根结点开始查找,把根结点设置为当前结点。
若当前结点为空,返回 null。
若当前结点不为空,用当前结点的 key 跟查找 key 作比较。
若当前结点 key 等于查找 key,那么该 key 就是查找目标,返回当前结点。
若当前结点 key 大于查找 key,把当前结点的左子结点设置为当前结点,重复步骤 2。
若当前结点 key 小于查找 key,把当前结点的右子结点设置为当前结点,重复步骤 2。
如图 5 所示:
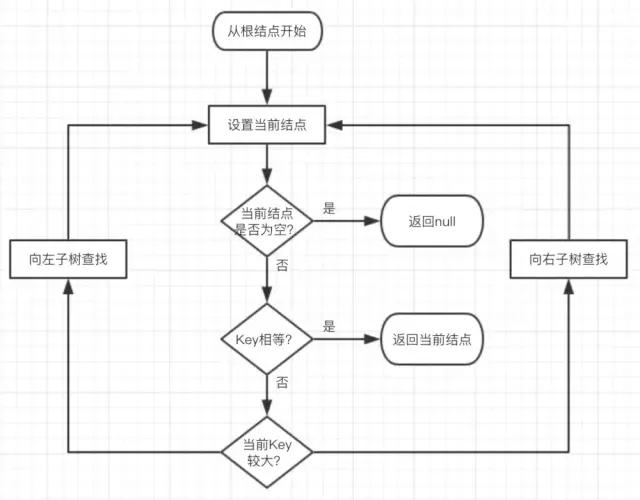
图 5:二叉树查找流程图
非常简单,但简单不代表它效率不好。正由于红黑树总保持黑色完美平衡,所以它的查找最坏时间复杂度为 O(2lgN),也即整颗树刚好红黑相隔的时候。
能有这么好的查找效率得益于红黑树自平衡的特性,而这背后的付出,红黑树的插入操作功不可没。
红黑树插入
插入操作包括两部分工作:一是查找插入的位置;二是插入后自平衡。
查找插入的父结点很简单,跟查找操作区别不大:
从根结点开始查找。
若根结点为空,那么插入结点作为根结点,结束。
若根结点不为空,那么把根结点作为当前结点。
若当前结点为 null,返回当前结点的父结点,结束。
若当前结点 key 等于查找 key,那么该 key 所在结点就是插入结点,更新结点的值,结束。
若当前结点 key 大于查找 key,把当前结点的左子结点设置为当前结点,重复步骤 4。
若当前结点 key 小于查找 key,把当前结点的右子结点设置为当前结点,重复步骤 4。
如图 6 所示:
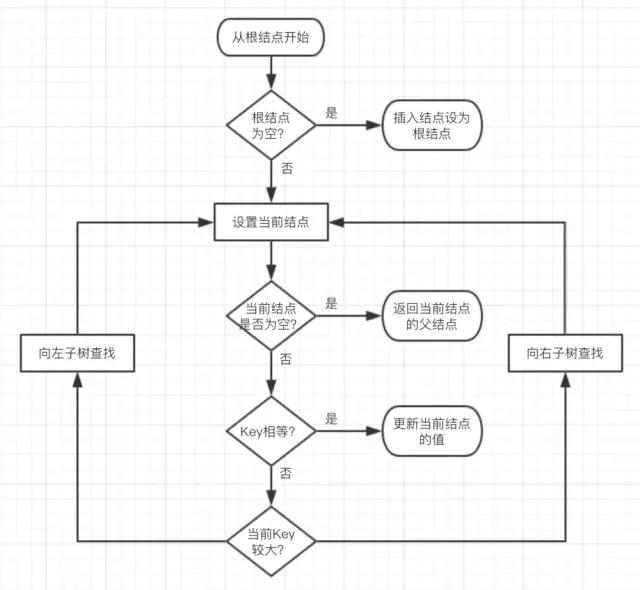
图 6:红黑树插入位置查找
OK,插入位置已经找到,把插入结点放到正确的位置就可以啦,但插入结点应该是什么颜色呢?
答案是红色。理由很简单,红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。
但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多 1,必须做自平衡。
所有插入情景如图 7 所示:
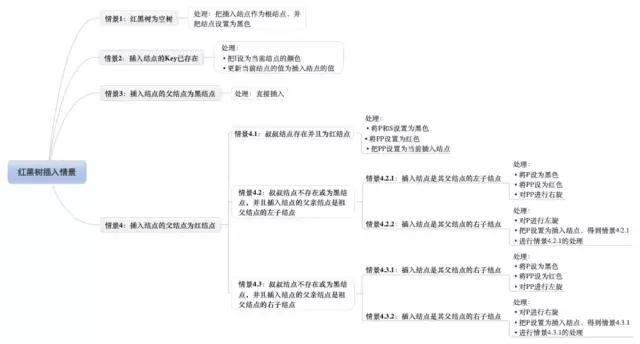
图 7:红黑树插入情景
嗯,插入情景很多呢,8 种插入情景!但情景 1、2 和 3 的处理很简单,而情景 4.2 和情景 4.3 只是方向反转而已。
懂得了一种情景就能推出另外一种情景,所以总体来看,并不复杂,后续我们将一个一个情景来看,把它彻底搞懂。
另外,根据二叉树的性质,除了情景 2,所有插入操作都是在叶子结点进行的。这点应该不难理解,因为查找插入位置时,我们就是在找子结点为空的父结点的。
在开始每个情景的讲解前,我们还是先来约定下,如图 8 所示:
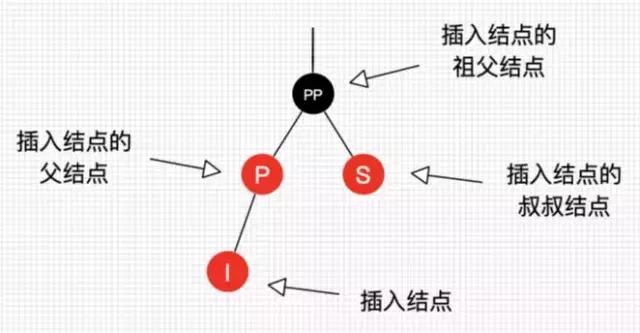
图 8:插入操作结点的叫法约定
图 8 的字母并不代表结点 Key 的大小。I 表示插入结点,P 表示插入结点的父结点,S 表示插入结点的叔叔结点,PP 表示插入结点的祖父结点。
好了,下面让我们一个一个来分析每个插入的情景以及处理。
情景 1:红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行,但注意,根据红黑树性质 2:根节点是黑色。还需要把插入结点设为黑色。
处理:把插入结点作为根结点,并把结点设置为黑色。
情景 2:插入结点的 Key 已存在
插入结点的 Key 已存在,既然红黑树总保持平衡,在插入前红黑树已经是平衡的,那么把插入结点设置为将要替代结点的颜色,再把结点的值更新就完成插入。
处理:把 I 设为当前结点的颜色,更新当前结点的值为插入结点的值。
情景 3:插入结点的父结点为黑结点
由于插入的结点是红色的,当插入结点是黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
处理:直接插入。
情景 4:插入结点的父结点为红结点

