再次回想下红黑树的性质 2:根结点是黑色。如果插入的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。这点很重要,因为后续的旋转操作肯定需要祖父结点的参与。
情景 4 又分为很多子情景,下面将进入重点部分,各位看官请留神了。
插入情景 4.1:叔叔结点存在并且为红结点。
从红黑树性质 4 可以,祖父结点肯定为黑结点,因为不可以同时存在两个相连的红结点。
那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红。如图 9 和图 10 所示。
处理:将 P 和 S 设置为黑色,将 PP 设置为红色,把 PP 设置为当前插入结点。
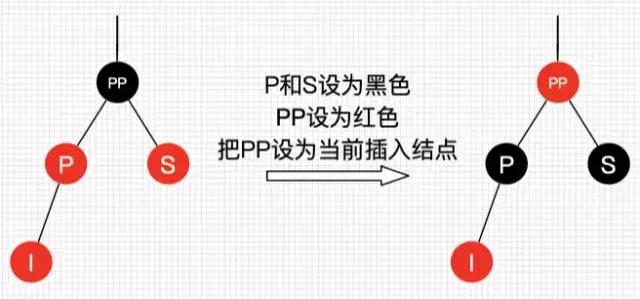
图 9:插入情景 4.1_1

图 10:插入情景 4.1_2
可以看到,我们把 PP 结点设为红色了,如果 PP 的父结点是黑色,那么无需再做任何处理。
但如果 PP 的父结点是红色,根据性质 4,此时红黑树已不平衡了,所以还需要把 PP 当作新的插入结点,继续做插入操作自平衡处理,直到平衡为止。
试想下 PP 刚好为根结点时,那么根据性质 2,我们必须把 PP 重新设为黑色,那么树的红黑结构变为:黑黑红。
换句话说,从根结点到叶子结点的路径中,黑色结点增加了。这也是唯一一种会增加红黑树黑色结点层数的插入情景。
我们还可以总结出另外一个经验:红黑树的生长是自底向上的。这点不同于普通的二叉查找树,普通的二叉查找树的生长是自顶向下的。
插入情景 4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点。
单纯从插入前来看,也即不算情景 4.1 自底向上处理时的情况,叔叔结点非红即为叶子结点(Nil)。
因为如果叔叔结点为黑结点,而父结点为红结点,那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了,这不满足红黑树的性质 5。后续情景同样如此,不再多做说明了。
前文说了,需要旋转操作时,肯定一边子树的结点多了或少了,需要租或借给另一边。插入显然是多的情况,那么把多的结点租给另一边子树就可以了。
插入情景 4.2.1:插入结点是其父结点的左子结点。
处理:将 P 设为黑色,将 PP 设为红色,对 PP 进行右旋。

图 11:插入情景 4.2.1
由图 11 可得,左边两个红结点,右边不存在,那么一边一个刚刚好,并且因为为红色,肯定不会破坏树的平衡。
咦,可以把 PP 设为红色,I 和 P 设为黑色吗?答案是可以!看过《算法:第 4 版》的同学可能知道,书中讲解的就是把 PP 设为红色,I 和 P 设为黑色。
但把 PP 设为红色,显然又会出现情景 4.1 的情况,需要自底向上处理,做多了无谓的操作,既然能自己消化就不要麻烦祖辈们啦。
插入情景 4.2.2:插入结点是其父结点的右子结点。
这种情景显然可以转换为情景 4.2.1,如图 12 所示,不做过多说明了。
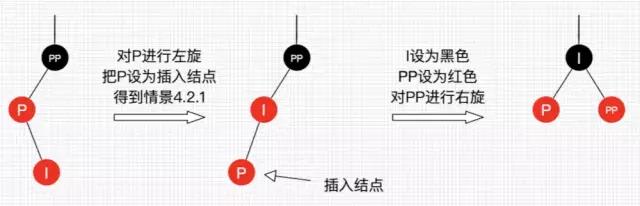
图 12:插入情景 4.2.2
处理:对 P 进行左旋,把 P 设置为插入结点,得到情景 4.2.1,进行情景 4.2.1 的处理。
插入情景 4.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点。
该情景对应情景 4.2,只是方向反转,不做过多说明了,直接看图。
插入情景 4.3.1:插入结点是其父结点的右子结点。

图 13:插入情景 4.3.1
处理:将 P 设为黑色,将 PP 设为红色,对 PP 进行左旋。
插入情景 4.3.2:插入结点是其父结点的右子结点。
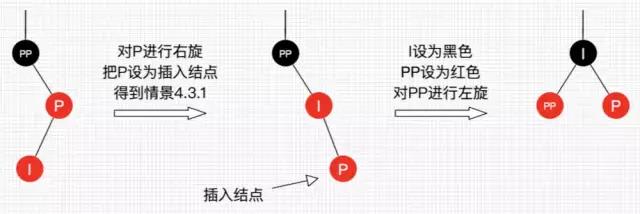
图 14:插入情景 4.3.2
处理:对 P 进行右旋,把 P 设置为插入结点,得到情景 4.3.1,进行情景 4.3.1 的处理。

