$X$的样本协方差矩阵
$$\left. \begin{array} { c } { S = [ s _ { i j } ] _ { m \times m } , \quad s _ { i j } = \frac { 1 } { n - 1 } \sum _ { k = 1 } ^ { n } ( x _ { i k } - \overline { x } _ { i } ) ( x _ { j k } - \overline { x } _ { j } ) } \ { i = 1,2 , \cdots , m , \quad j = 1,2 , \cdots , m } \end{array} \right.$$
给定样本数据矩阵$X$,考虑向量$x$到$y$的线性变换$$y = A ^ { T } x$$
这里
$$A = \left[ \begin{array} { l l l l } { a _ { 1 } } & { a _ { 2 } } & { \cdots } & { a _ { m } } \end{array} \right] = \left[ \begin{array} { c c c c } { a _ { 11 } } & { a _ { 12 } } & { \cdots } & { a _ { 1 m } } \ { a _ { 21 } } & { a _ { 22 } } & { \cdots } & { a _ { 2 m } } \ { \vdots } & { \vdots } & { } & { \vdots } \ { a _ { m 1 } } & { a _ { m 2 } } & { \cdots } & { a _ { m m } } \end{array} \right]$$
如果该线性变换满足以下条件,则称之为样本主成分。样本第一主成分$y _ { 1 } = a _ { 1 } ^ { T } x$是在$a _ { 1 } ^ { T } a _ { 1 } = 1$条件下,使得$a _ { 1 } ^ { T } x _ { j } ( j = 1,2 , \cdots , n )$的样本方差$a _ { 1 } ^ { T } S a _ { 1 }$最大的$x$的线性变换;
样本第二主成分$y _ { 2 } = a _ { 2 } ^ { T } x$是在$a _ { 2 } ^ { T } a _ { 2 } = 1$和$a _ { 2 } ^ { T } x _ { j }$与$a _ { 1 } ^ { T } x _ { j } ( j = 1,2 , \cdots , n )$的样本协方差$a _ { 1 } ^ { T } S a _ { 2 } = 0$条件下,使得$a _ { 2 } ^ { T } x _ { j } ( j = 1,2 , \cdots , n )$的样本方差$a _ { 2 } ^ { T } S a _ { 2 }$最大的$x$的线性变换;
一般地,样本第$i$主成分$y _ { i } = a _ { i } ^ { T } x$是在$a _ { i } ^ { T } a _ { i } = 1$和$a _ { i } ^ { T } x _ { j }$与$a _ { k } ^ { T } x _ { j } ( k < i , j = 1,2 , \cdots , n )$的样本协方差$a _ { k } ^ { T } S a _ { i } = 0$条件下,使得$a _ { i } ^ { T } x _ { j } ( j = 1,2 , \cdots , n )$的样本方差$a _ { k } ^ { T } S a _ { i }$最大的$x$的线性变换。
5.主成分分析方法主要有两种,可以通过相关矩阵的特征值分解或样本矩阵的奇异值分解进行。
(1)相关矩阵的特征值分解算法。针对$m \times n$样本矩阵$X$,求样本相关矩阵
$$R = \frac { 1 } { n - 1 } X X ^ { T }$$
再求样本相关矩阵的$k$个特征值和对应的单位特征向量,构造正交矩阵
$$V = ( v _ { 1 } , v _ { 2 } , \cdots , v _ { k } )$$
$V$的每一列对应一个主成分,得到$k \times n$样本主成分矩阵
$$Y = V ^ { T } X$$
(2)矩阵$X$的奇异值分解算法。针对$m \times n$样本矩阵$X$
$$X ^ { \prime } = \frac { 1 } { \sqrt { n - 1 } } X ^ { T }$$
对矩阵$X ^ { \prime }$进行截断奇异值分解,保留$k$个奇异值、奇异向量,得到
$$X ^ { \prime } = U S V ^ { T }$$
$V$的每一列对应一个主成分,得到$k \times n$样本主成分矩阵$Y$
$$Y = V ^ { T } X$$
输入:n维样本集$D=(x^{(1)}, x{(2)},...,x{(m)})$,要降维到的维数n'.
输出:降维后的样本集$D'$
1、 对所有的样本进行中心化:
$x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}{m} x{(j)}$
2、 计算样本的协方差矩阵$XX^T$
3、 对矩阵$XX^T$进行特征值分解
4、 取出最大的n'个特征值对应的特征向量$(w_1,w_2,...,w_{n'})$, 将所有的特征向量标准化后,组成特征向量矩阵W。
5、 对样本集中的每一个样本$x{(i)}$,转化为新的样本$z{(i)}=WTx{(i)}$
6、 得到输出样本集$D' =(z^{(1)}, z{(2)},...,z{(m)})$
有时候,我们不指定降维后的n'的值,而是换种方式,指定一个降维到的主成分比重阈值t。这个阈值t在(0,1]之间。假如我们的n个特征值为$\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_n$,则n'可以通过下式得到:$$\frac{\sum\limits_{i=1}{n'}\lambda_i}{\sum\limits_{i=1}{n}\lambda_i} \geq t $$
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)
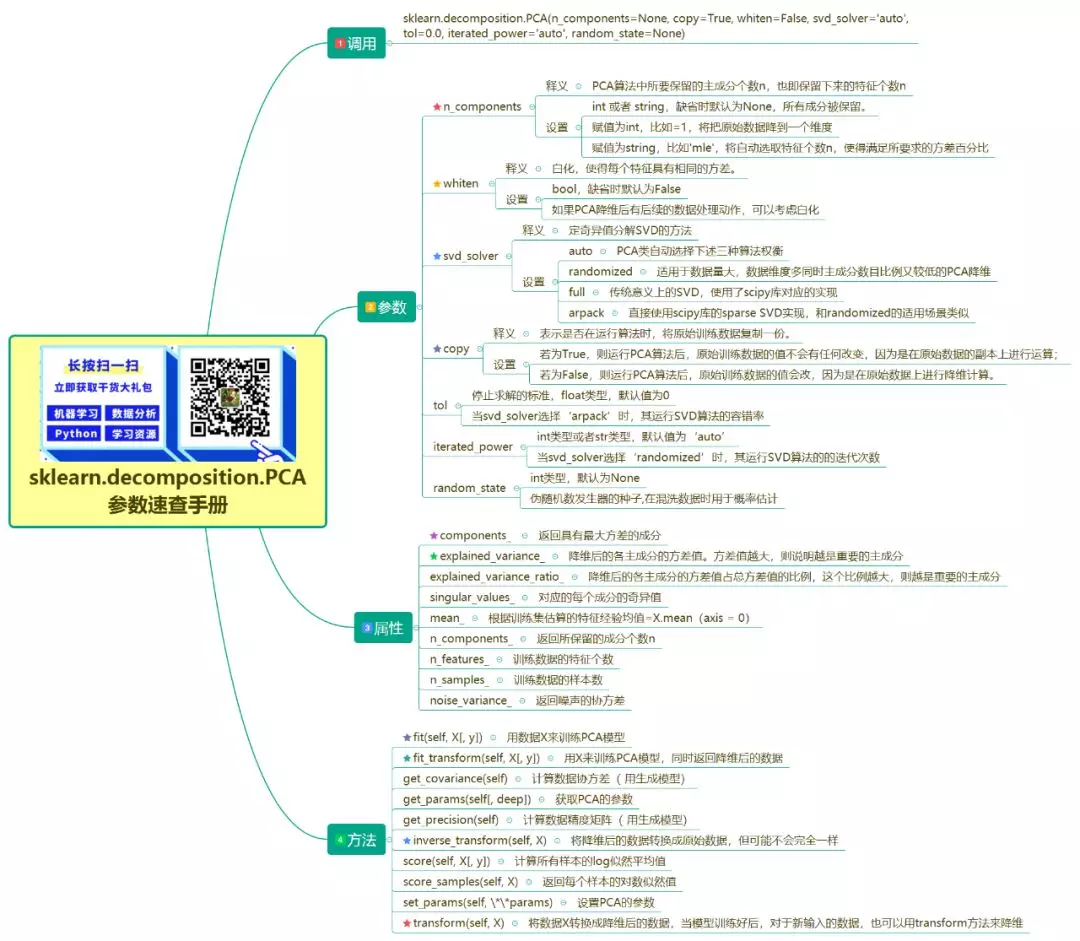
PCA 的使用简单的离谱,一般指定n_components即可,如果设置为整数,说明要保留的主成分数量。如果将其设置为小数,则说明降维后的数据能保留的信息。
上面提到主成分分析方法主要有两种,可以通过相关矩阵的特征值分解或样本矩阵的奇异值分解$A = U\Sigma V^T$进行。scikit-learn库的PCA使用的就是奇异值分解方法,通过svd_solver参数指定:
randomized:适用于数据量大,数据维度多同时主成分数目比例又较低的 PCA 降维
full:传统意义上的 SVD,使用了 scipy 库对应的实现

