100天搞定机器学习|Day59 主成分分析(PCA)原理及使用详解 (3)

arpack：直接使用 scipy 库的 sparse SVD 实现，和 randomized 的适用场景类似

import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from sklearn.decomposition import PCA from sklearn.datasets.samples_generator import make_blobs X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3, 3, 3], [0, 0, 0], [1, 1, 1], [2, 2, 2]], cluster_std=[0.2, 0.1, 0.2, 0.2], random_state=9) fig = plt.figure() plt.scatter(X_new[:, 0], X_new[:, 1], marker='o') plt.show()

# 降维到二维 pca = PCA(n_components=2) pca.fit(X) # 输出特征值 print(pca.explained_variance_) 输出特征向量 print(pca.components_) # 降维后的数据 X_new = pca.transform(X) print(X_new) fig = plt.figure() plt.scatter(X_new[:, 0], X_new[:, 1], marker='o') plt.show()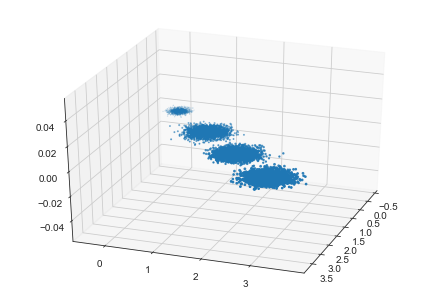

这样我们就实现了三维到二维的转换，可以把结果可视化：

PCA算法优缺点

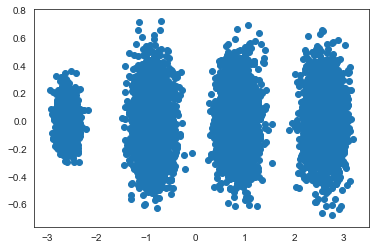
PCA算法优点

1，仅仅需要以方差衡量信息量，不受数据集以外的因素影响

2，各主成分之间正交，可消除原始数据成分间的相互影响的因素

3，计算方法简单，主要运算时特征值分解，易于实现

4，它是无监督学习，完全无参数限制的。

PCA算法缺点

1，主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强

2，方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

参考

https://github.com/fengdu78/lihang-code
https://finthon.com/python-pca/
https://www.cnblogs.com/pinard/p/6239403.html