本题中合法括号串的定义如下:
() 是合法括号串。
如果 A 是合法括号串,则 (A) 是合法括号串。
如果 A,B 是合法括号串,则 AB 是合法括号串。
本题中子串与不同的子串的定义如下:
字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 \(l\) 与终止位置 \(r\) 来表示,记为 S (l, r)(\(1 \leq l \leq r \leq |S |\)\(|S |\) 表示 \(S\) 的长度)。
S 的两个子串视作不同当且仅当它们在 S 中的位置不同,即 \(l\) 不同或 \(r\) 不同。
题目描述一个大小为 \(n\) 的树包含 \(n\) 个结点和 \(n − 1\) 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
小 \(Q\) 是一个充满好奇心的小朋友,有一天他在上学的路上碰见了一个大小为 \(n\) 的树,树上结点从 \(1\) ∼ \(n\) 编号,\(1\) 号结点为树的根。除 \(1\) 号结点外,每个结点有一个父亲结点,\(u\)(\(2 \leq u \leq n\))号结点的父亲为 \(f_u\)(\(1 ≤ f_u < u\))号结点。
小 \(Q\) 发现这个树的每个结点上恰有一个括号,可能是( 或)。小 \(Q\) 定义 \(s_i\) 为:将根结点到 \(i\) 号结点的简单路径上的括号,按结点经过顺序依次排列组成的字符串。
显然 \(s_i\) 是个括号串,但不一定是合法括号串,因此现在小 \(Q\) 想对所有的 \(i\)(\(1\leq i\leq n\))求出,\(s_i\) 中有多少个互不相同的子串是合法括号串。
这个问题难倒了小 \(Q\),他只好向你求助。设 \(s_i\) 共有 \(k_i\) 个不同子串是合法括号串, 你只需要告诉小 Q 所有 \(i \times k_i\) 的异或和,即:
\((1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n)\)
其中 \(xor\) 是位异或运算。
输入格式第一行一个整数 \(n\),表示树的大小。
第二行一个长为 \(n\) 的由( 与) 组成的括号串,第 \(i\) 个括号表示 \(i\) 号结点上的括号。
第三行包含 \(n − 1\) 个整数,第 \(i\)(\(1 \leq i \lt n\))个整数表示 \(i + 1\) 号结点的父亲编号 \(f_{i+1}\)。
输出格式仅一行一个整数表示答案。
输入输出样例输入 #1
5 (()() 1 1 2 2输出 #1
6 说明/提示【样例解释1】
树的形态如下图:
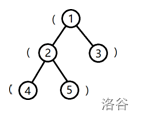
将根到 \(1\) 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (,子串是合法括号串的个数为 \(0\)。
将根到 \(2\) 号结点的字符串为 ((,子串是合法括号串的个数为 \(0\)。
将根到 \(3\) 号结点的字符串为 (),子串是合法括号串的个数为 \(1\)。
将根到 \(4\) 号结点的字符串为 (((,子串是合法括号串的个数为 \(0\)。
将根到 \(5\) 号结点的字符串为 ((),子串是合法括号串的个数为 \(1\)。
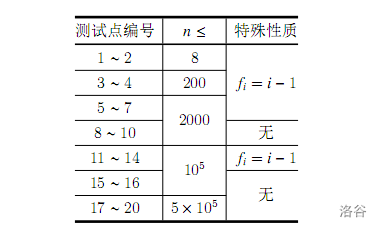
【数据范围】
明显的树形\(DP\)。
思路有点难讲。花了考场上\(1.5h\)想出来的。
先考虑暴力。我们需要一个能过\(50pts\)的暴力,所以对于每一个节点,我们必须在最多\(O(n)\)的时间处理出答案贡献。
考虑类似单调性优化的方法。容易想到,对于一个点\(u\)的父亲,当它转移到\(u\)时,所增加的合法子串数量只有这个括号加上从这个点到之前链上所有括号的匹配情况。
比如说我们加了一个右括号,我只需要往回搜索所有合法的每个链上的左括号即可。由此,我们需要用\(O(1)\)的时间检查每个左括号是否能对新加入的右括号作出贡献。
我们需要用一个栈记录所有没有匹配过的右括号。每次遇到一个右括号就把它进栈;每次遇到左括号如果栈空直接\(break\),因为再往前搜的字串一定经过这个不可能匹配到的左括号;否则把它出栈,如果出栈之后栈空说明从这个位置到新加入的位置恰好构成一个合法串,答案加一。
这个复杂度是\(O(n)\)的主要原因是对于每一个点必须扫描所有前面的点,这个过程效率实在太低。考虑优化这个过程。
对于每一个新进入栈的右括号,能对答案做出的贡献只有两种情况:

