机器学习数学基础:学习线性代数,千万不要误入歧途!推荐一个正确学习路线

写完《机器学习深度研究:机器学习中的高等数学/微积分及Python实现》,觉得十分对不起读者,写的自己都不满意。
就像前篇所说,这种极度基础的知识是最难介绍的,我也在思考如何转变方式,把问题讲清楚。但是头条是不支持数学公式的,篇幅也受限。所以本篇文章,我想介绍一下自己的学习历程,看过不错的教材和视频推荐给大家。这样大家也能少走弯路,更全面的学到知识。
同时建议:贪多嚼不烂,求精不求多,我有自信,看过我推荐的这本书和视频,线性代数就绝对可以搞定了。
机器学习中的线性代数线性代数是机器学习领域不可或缺的一部分,从描述算法操作的符号到代码中算法的实现,都属于线性代的研究范围。线性代数在机器学习的几乎所有地方都有使用,具体用到的知识点有:
向量和它的各种运算,包括加法,减法,数乘,转置,内积
向量和矩阵的范数,L1范数和L2范数
矩阵和它的各种运算,包括加法,减法,乘法,数乘
逆矩阵的定义与性质
行列式的定义与计算方法
二次型的定义
矩阵的正定性
矩阵的特征值与特征向量
矩阵的奇异值分解
线性方程组的数值解法,尤其是共轭梯度法
教材推荐学习线性代数,你可千万不要掏出同济大学版的教材出来,这本书非常糟糕,它只适合考试复习用。

我推荐《Linear Algebra Review and Reference》

本资料为CS229 Andrew Ng-Mechine Learning课程关于线性代数的复习讲义。
英文不好的同学也不用担心,已经有大佬将其翻译成中文了,目录如下:
基础概念和符号
1.1 基本符号
2.矩阵乘法
2.1 向量-向量乘法
2.2 矩阵-向量乘法
2.3 矩阵-矩阵乘法
3 运算和属性
3.1 单位矩阵和对角矩阵
3.2 转置
3.3 对称矩阵
3.4 矩阵的迹
3.5 范数
3.6 线性相关性和秩
3.7 方阵的逆
3.8 正交阵
3.9 矩阵的值域和零空间
3.10 行列式
3.11 二次型和半正定矩阵
3.12 特征值和特征向量
3.13 对称矩阵的特征值和特征向量
4.矩阵微积分
4.1 梯度
4.2 黑塞矩阵
4.3 二次函数和线性函数的梯度和黑塞矩阵
4.4 最小二乘法
4.5 行列式的梯度
4.6 特征值优化
如需电子版请私信我:线性代数 wx:htsa360
视频推荐有些同学更喜欢看视频,这里我吹爆一门由大名鼎鼎的3blue1brown出品的教程:《线性代数的本质》,3blue1brown的课程,动画精美,讲解生动,非常适合帮助建立数学的形象思维,值得反复观看。
看过之后我相信你会发出这样的感慨:我以前学的线性代数是什么鬼呀!
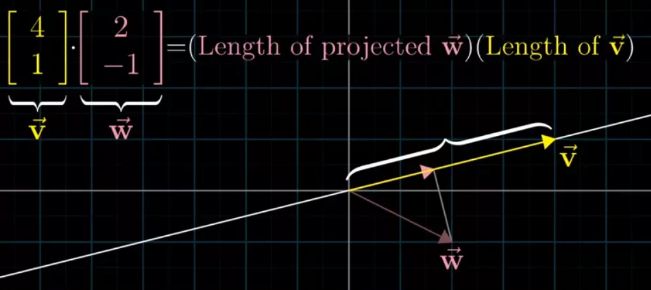
举个例子,叉积这个概念在机器学习中应用不能更广泛,3B1B对它的解释:把w投射到v所在的直线上,将w在v上投影的长度乘以v的长度,就是其点积的值
想要观看的同学可以去B站搜索:av6731067


