AVL树(二叉平衡树)详解与实现 (2)

因为对于右左结构，中间的最大，两侧的最小。但是下面的比上面大(下面在上面右侧)所以如果平衡的话，那么右左的R.L应该在中间，而R应该在右侧。原来的root在左侧。

所以节点的变化浮动比较大，而且需要妥善处理各个子节点的移动使其满足二叉排序树的性质！

期间考虑树高度变化即可！

这种双旋转其实也很简单。不要被外表唬住。基于前面的单旋转，双旋转有两种具体逻辑思路。
思路1：两次旋转RR,LL

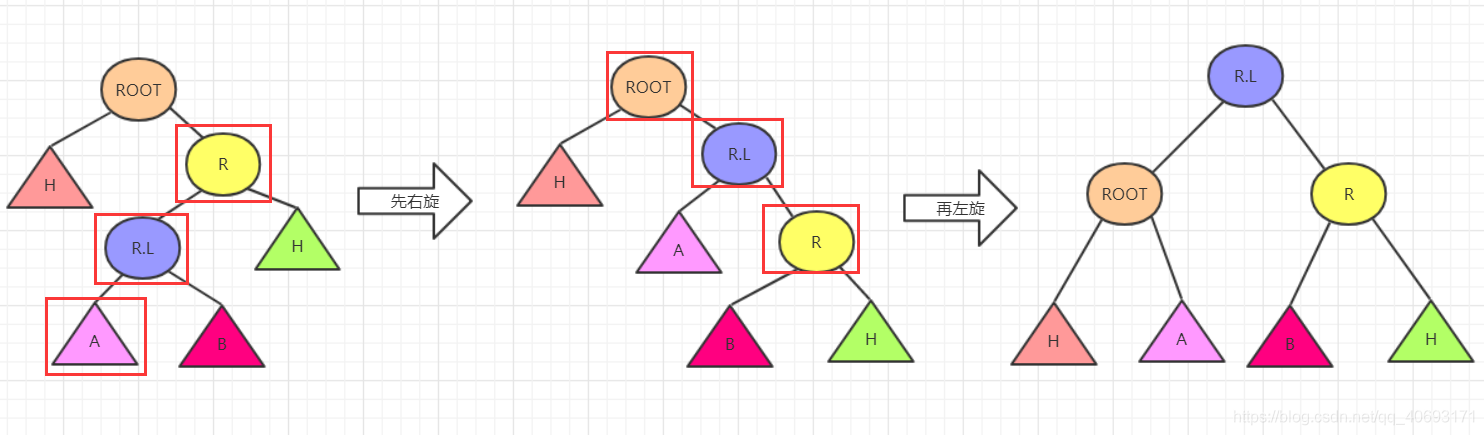
根据上图所圈的，先对底部使得底部的大小关系变化，使其在满足二叉平衡树的条件下还满足RR结构的二叉树。所以只需要对右节点R先进行右旋,再对ROOT进行左旋即可。
思路2：直接分析
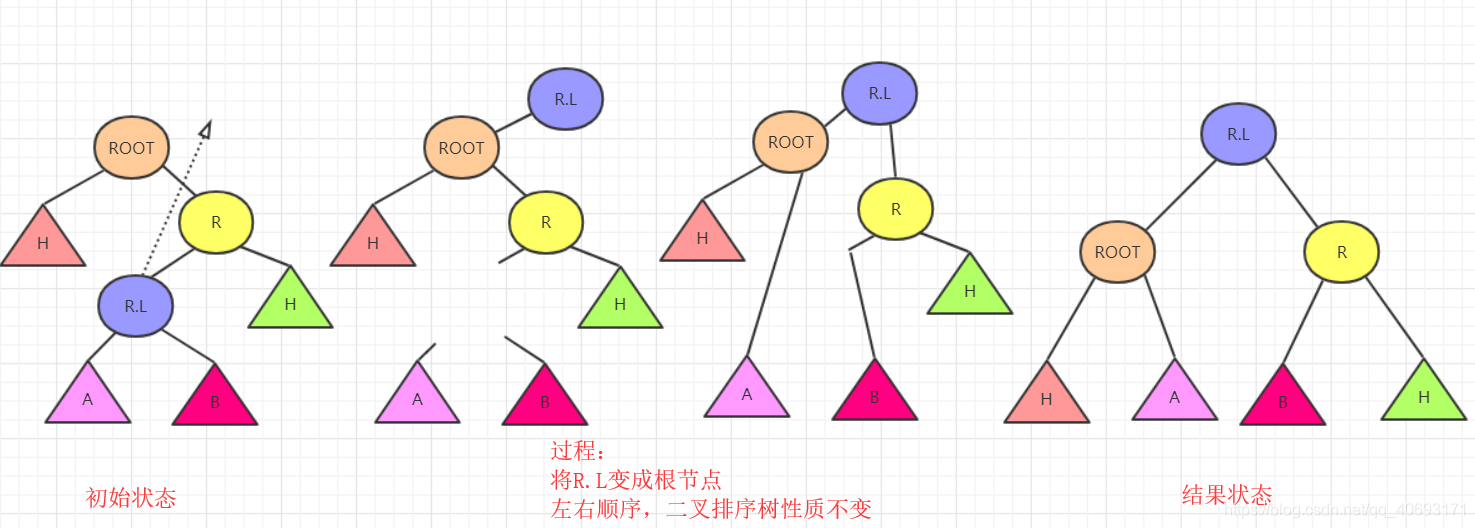
根据初始和结果的状态，然后分析各个节点变化顺序。手动操作这些节点即可！

首先根据ROOT,R,R.L三个节点变化。R.L肯定要在最顶层。左右分别指向ROOT和R。那么这其中R.left，ROOT.right发生变化(原来分别是R,L和R)暂时为空。而刚好根据左右大小关系可以补上R.L的左右节点。

这样思考整棵树也可以完成平衡，但是要考虑树的高度变化。

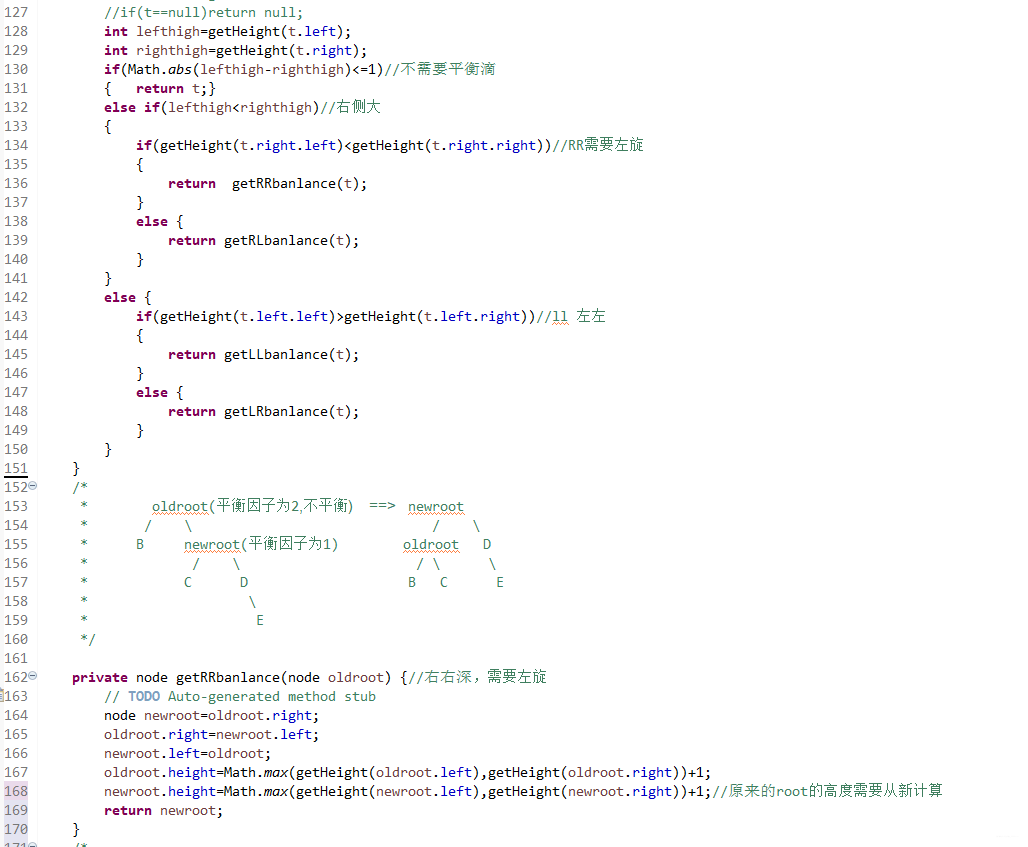
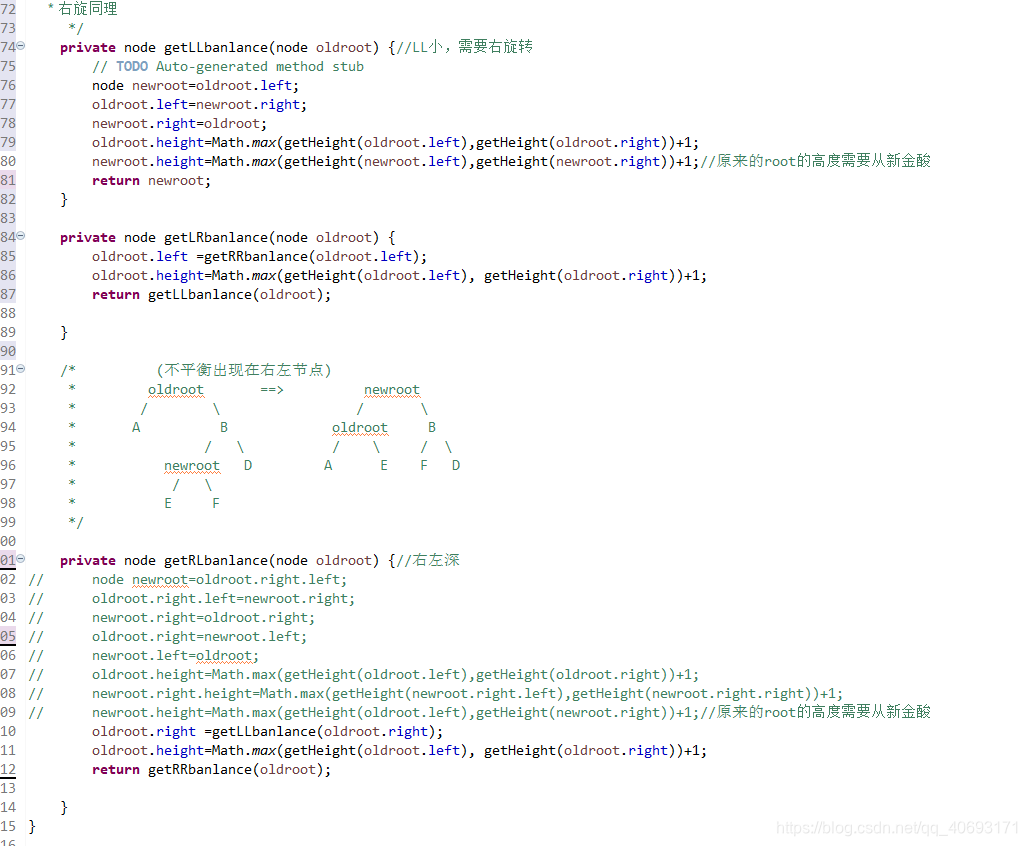
代码为：(注释部分为方案1)

private node getRLbanlance(node oldroot) {//右左深 // node newroot=oldroot.right.left; // oldroot.right.left=newroot.right; // newroot.right=oldroot.right; // oldroot.right=newroot.left; // newroot.left=oldroot; // oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; // newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1; // newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸 oldroot.right =getLLbanlance(oldroot.right); oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1; return getRRbanlance(oldroot); } LR平衡旋转(先左后右单旋转)

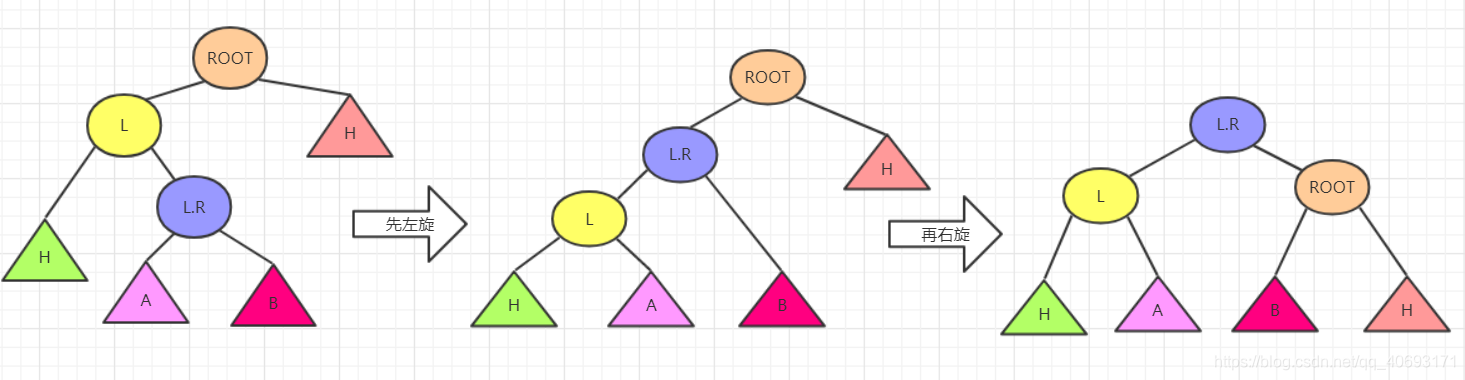
根据上述RL修改即可

private node getLRbanlance(node oldroot) { oldroot.left =getRRbanlance(oldroot.left); oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1; return getLLbanlance(oldroot); } java代码实现

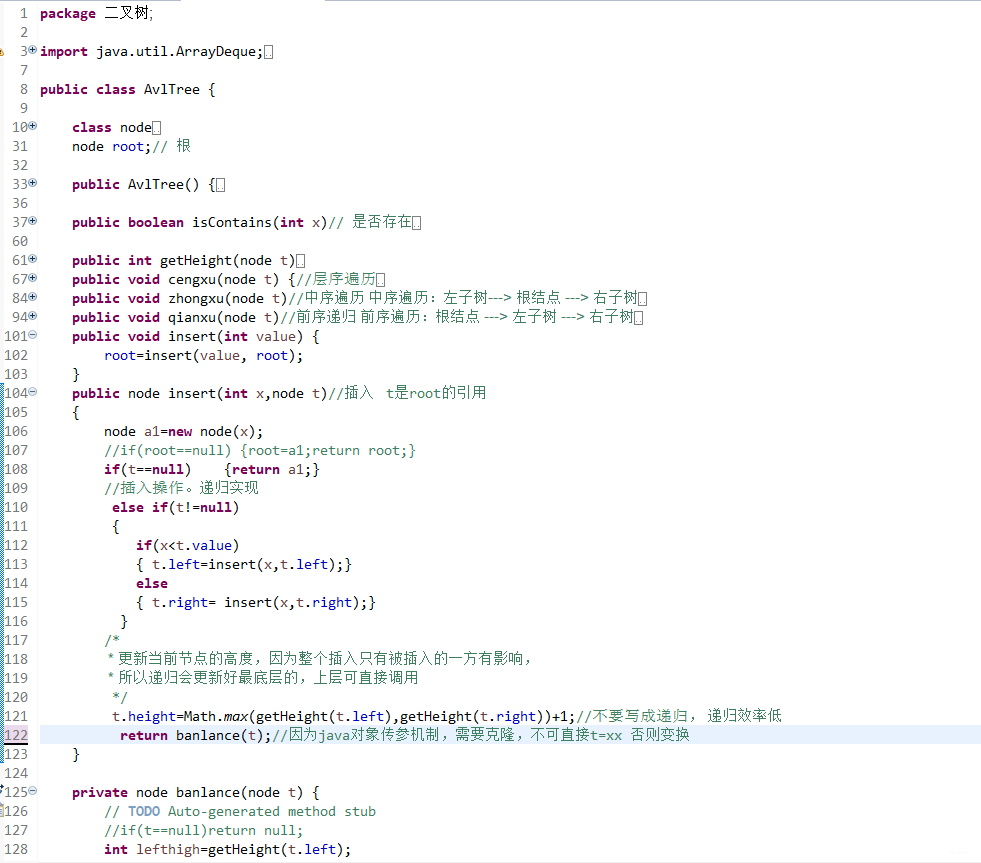
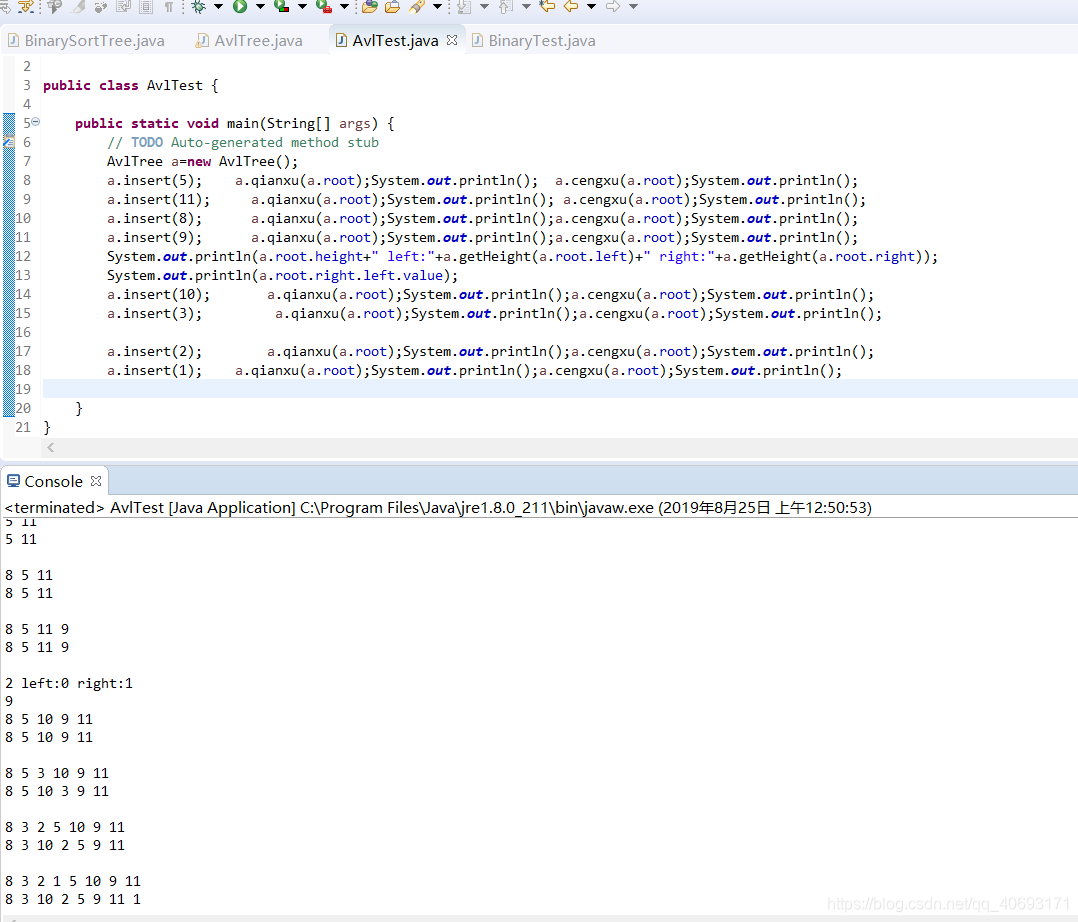
首先对于节点多个height属性。用于计算高度(平衡因子)

插入是递归插入。递归一个来回的过程，去的过程进行插入。回的过程进行高度更新。和检查是否平衡。不要写全局递归计算高度，效率太低下。事实上高度变化只和插入和平衡有关，仔细考虑即不会有疏漏！

总结 测试情况：

AVL的理解需要时间，当然笔者的AVL自己写的可能有些疏漏，如果有问题还请各位一起探讨！

当然，除了插入，AVL还有删除等其他操作，(原理相似。删除后平衡)有兴趣可以一起研究。

如果需要源码还请关注笔者公众号：公众号查看相关专题文章！