首发公众号:bigsai 转载需注明公众号和出处。
前言在排序算法中,快排是占比非常多的一环,但是快排其思想一直被考察研究,也有很多的优化方案。这里主要讲解双轴快排的思想和实现。
首选,双轴快排也是一种快排的优化方案,在JDK的Arrays.sort()中被主要使用。所以,掌握快排已经不能够满足我们的需求,我们还要学会双轴快排的原理和实现才行。
回顾单轴快排单轴快排也就是我们常说的普通快速排序,对于快速排序我想大家应该都很熟悉:基于递归和分治的,时间复杂度最坏而O(n2),最好和平均情况为O(nlogn).
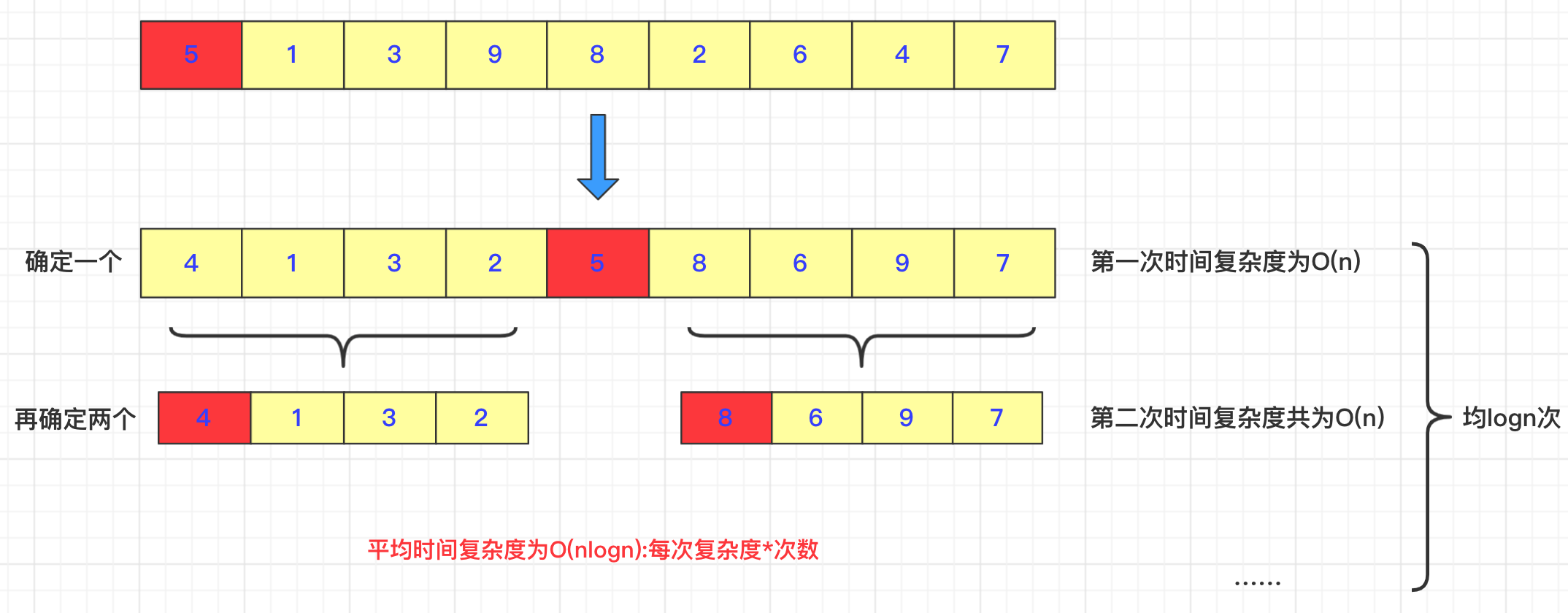
而快排的具体思路也很简单,每次在待排序序列中找一个数(通常最左侧多一点),然后在这个序列中将比他小的放它左侧,比它大的放它右侧。
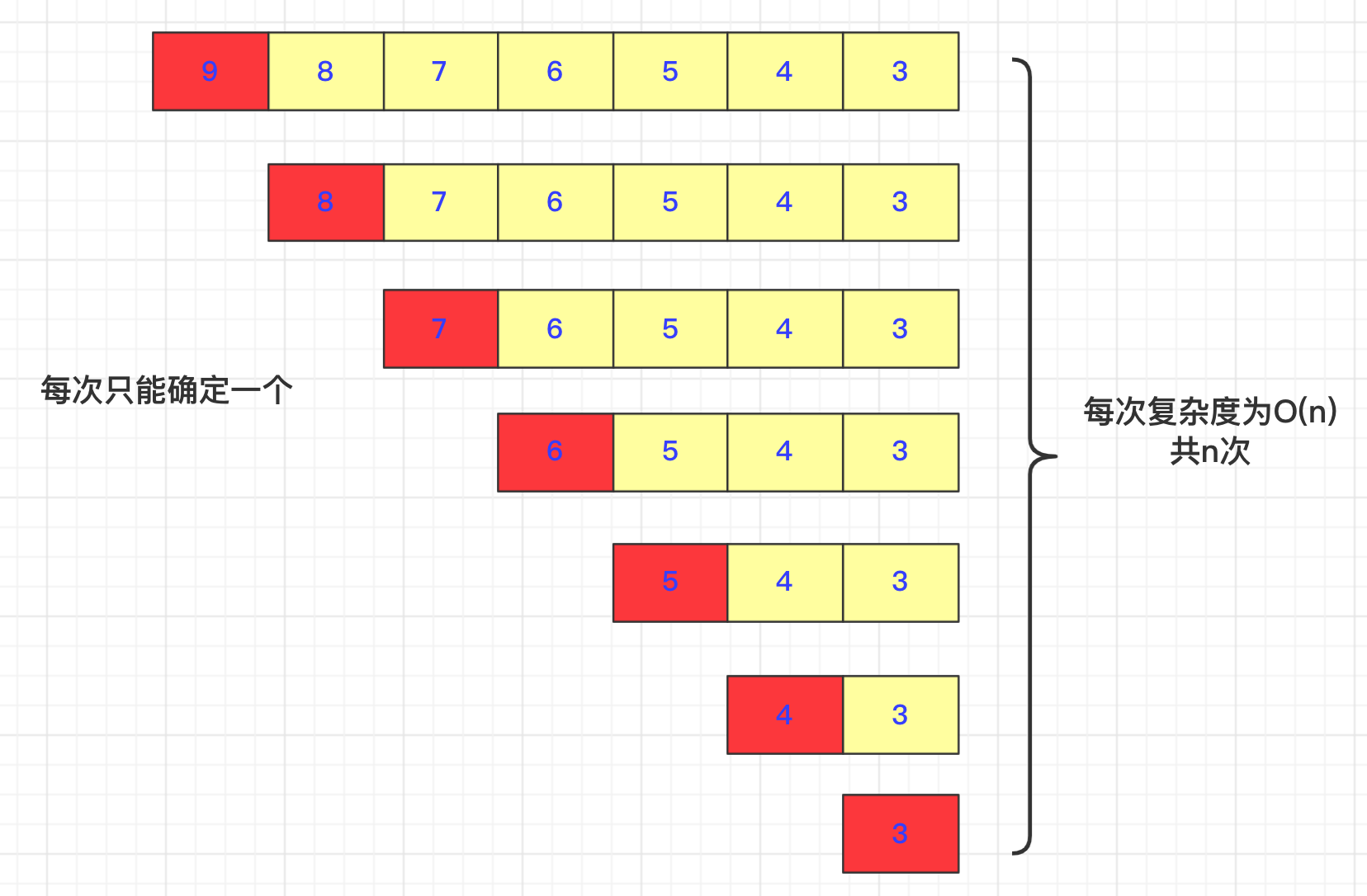
如果运气肯不好遇到O(n)平方的,那确实就很被啦:
实现起来也很容易,这里直接贴代码啦:
private static void quicksort(int [] a,int left,int right) { int low=left; int high=right; //下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!! if(low>high)//作为判断是否截止条件 return; int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。 while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。 { while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止 { high--; } //这样就找到第一个比它小的了 a[low]=a[high];//放到low位置 while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置 { low++; } a[high]=a[low]; } a[low]=k;//赋值然后左右递归分治求之 quicksort(a, left, low-1); quicksort(a, low+1, right); } 双轴快排分析咱们今天的主题是双轴快排,双轴和单轴的区别你也可以知道,多一个轴,前面讲了快排很多时候选最左侧元素以这个元素为轴将数据划分为两个区域,递归分治的去进行排序。但单轴很多时候可能会遇到较差的情况就是当前元素可能是最大的或者最小的,这样子元素就没有被划分区间,快排的递推T(n)=T(n-1)+O(n)从而为O(n2).
双轴就是选取两个主元素理想将区间划为3部分,这样不仅每次能够确定元素个数增多为2个,划分的区间由原来的两个变成三个,最坏最坏的情况就是左右同大小并且都是最大或者最小,但这样的概率相比一个最大或者最小还是低很多很多,所以双轴快排的优化力度还是挺大的。
总体情况分析至于双轴快排具体是如何工作的呢?其实也不难理解,这里通过一系列图讲解双轴快排的执行流程。
首先在初始的情况我们是选取待排序区间内最左侧、最右侧的两个数值作为pivot1和pivot2 .作为两个轴的存在。同时我们会提前处理数组最左侧和最右侧的数据会比较将最小的放在左侧。所以pivot1<pivot2.
而当前这一轮的最终目标是,比privot1小的在privot1左侧,比privot2大的在privot2右侧,在privot1和privot2之间的在中间。
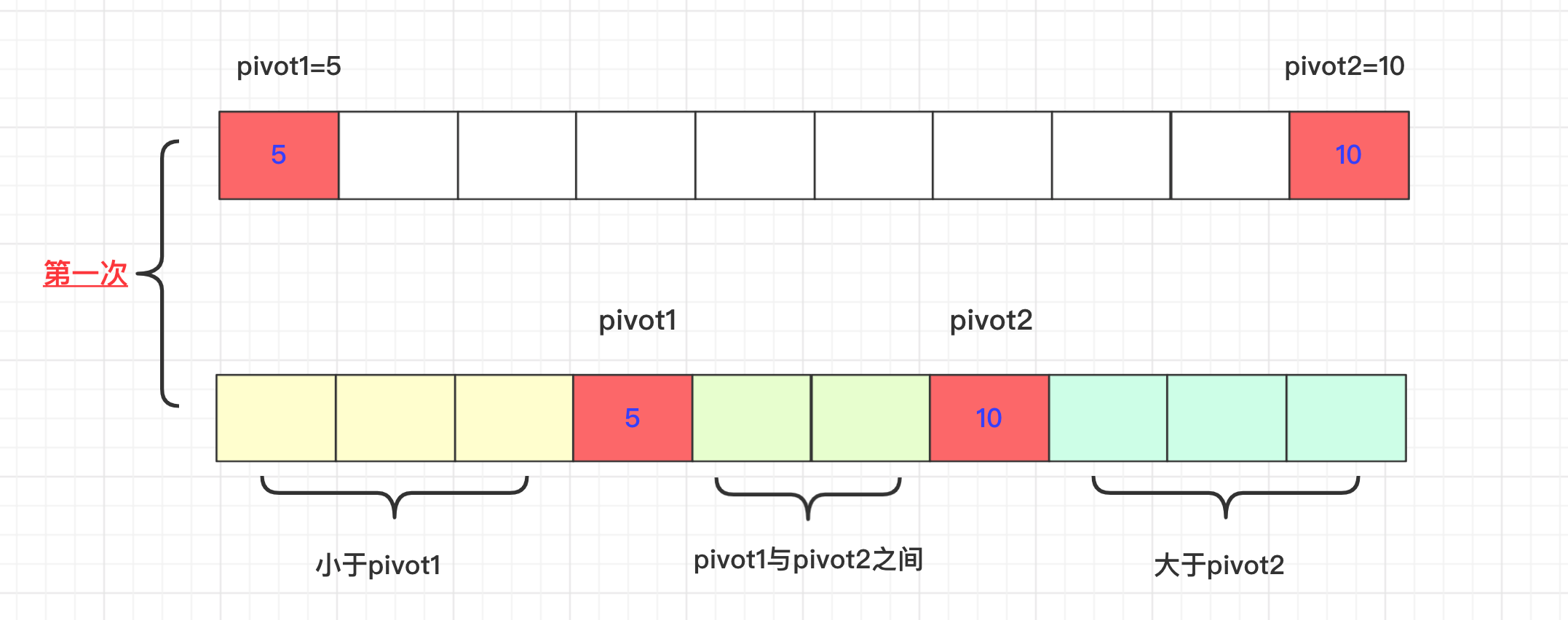
这样进行一次后递归的进行下一次双轴快排,一直到结束,但是在这个执行过程应该去如何处理分析呢?需要几个参数呢?
假设知道排序区间[start,end]。数组为arr, pivot1=arr[start],pivot2=arr[end]
还需要三个参数left,right和k。 l
left初始为start,[start,left]区域即为小于等于pivot1小的区域(第一个等于)。
right与left对应,初始为end,[right,end]为大于等于pivot2的区域(最后一个等于)。
k初始为start+1,是一个从左往右遍历的指针,遍历的数值与pivot1,pivot2比较进行适当交换,当k>=right即可停止。
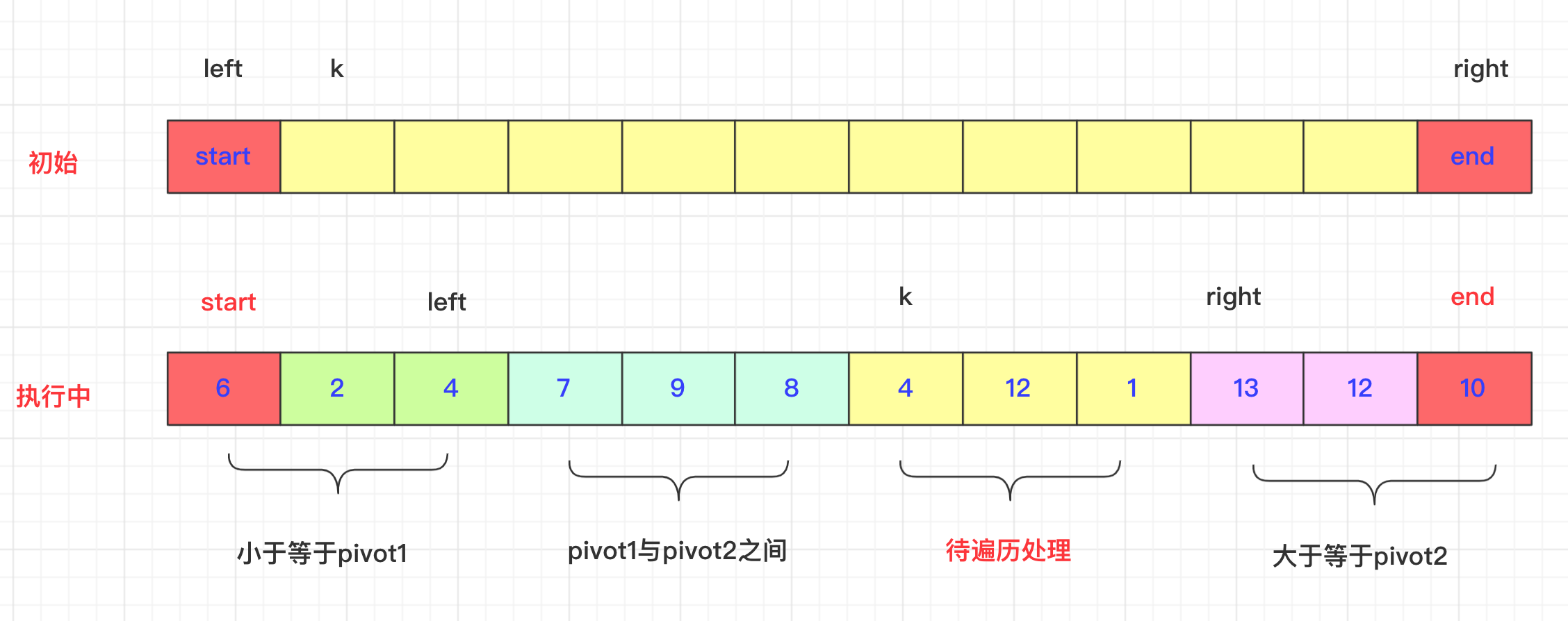
然后你可能会问k遍历时候究竟怎么去交换?left和right该如何处理呢?不急我带你慢慢分析,首先K是在left和right中间的,遍历k的位置和pivot1,pivot2进行比较:
如果arr[k]<pivot1,那么先++left,然后swap(arr,k,left),因为初始在start在这个过程不结束start先不动。然后k++;继续进行