这是 leetcode 的 62 号题:https://leetcode-cn.com/problems/unique-paths/
这道题的 dp 转移公式是 dp[i] [j] = dp[i-1] [j] + dp[i] [j-1],代码如下
不懂的看我之前文章:告别动态规划,连刷40道动规算法题,我总结了动规的套路
public static int uniquePaths(int m, int n) { if (m <= 0 || n <= 0) { return 0; } int[][] dp = new int[m][n]; // // 初始化 for(int i = 0; i < m; i++){ dp[i][0] = 1; } for(int i = 0; i < n; i++){ dp[0][i] = 1; } // 推导出 dp[m-1][n-1] for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { dp[i][j] = dp[i-1][j] + dp[i][j-1]; } } return dp[m-1][n-1]; }这种做法的空间复杂度是 O(n * m),下面我们来讲解如何优化成 O(n)。
dp[i] [j] 是一个二维矩阵,我们来画个二维矩阵的图,对矩阵进行初始化

然后根据公式 dp[i][j] = dp[i-1][j] + dp[i][j-1] 来填充矩阵的其他值。下面我们先填充第二行的值。
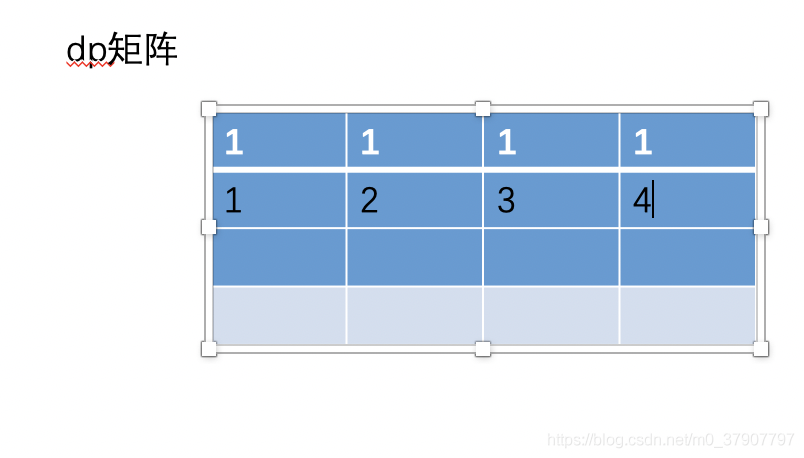
大家想一个问题,当我们要填充第三行的值的时候,我们需要用到第一行的值吗?答是不需要的,不行你试试,当你要填充第三,第四....第 n 行的时候,第一行的值永远不会用到,只要填充第二行的值时会用到。
根据公式 dp[i][j] = dp[i-1][j] + dp[i][j-1],我们可以知道,当我们要计算第 i 行的值时,除了会用到第 i - 1 行外,其他第 1 至 第 i-2 行的值我们都是不需要用到的,也就是说,对于那部分用不到的值我们还有必要保存他们吗?
答是没必要,我们只需要用一个一维的 dp[] 来保存一行的历史记录就可以了。然后在计算机的过程中,不断着更新 dp[] 的值。单说估计你可能不好理解,下面我就手把手来演示下这个过程。
1、刚开始初始化第一行,此时 dp[0..n-1] 的值就是第一行的值。

2、接着我们来一边填充第二行的值一边更新 dp[i] 的值,一边把第一行的值抛弃掉。
为了方便描述,下面我们用arr (i,j)表示矩阵中第 i 行 第 j 列的值。从 0 开始哈,就是说有第 0 行。
(1)、显然,矩阵(1, 0) 的值相当于以往的初始化值,为 1。然后这个时候矩阵 (0,0)的值不在需要保存了,因为再也用不到了。
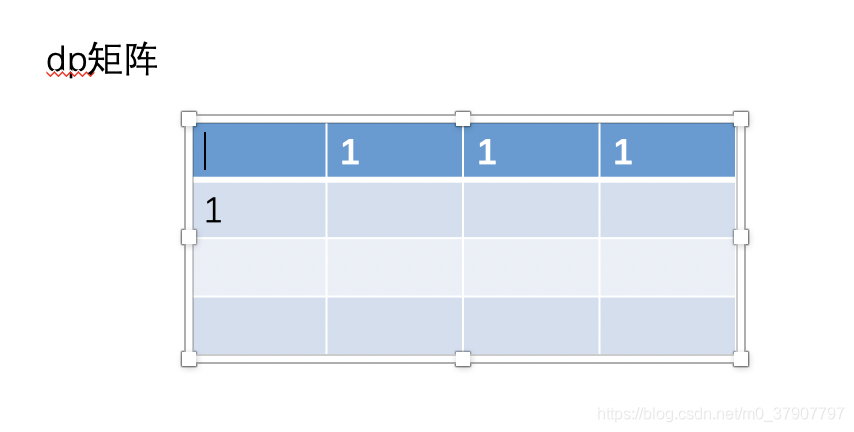
这个时候,我们也要跟着更新 dp[0] 的值了,刚开始 dp[0] = (0, 0),现在更新为 dp[0] = (1, 0)。
(2)、接着继续更新 (1, 1) 的值,根据之前的公式 (i, j) = (i-1, j) + (i, j- 1)。即 (1,1)=(0,1)+(1,0)=2。
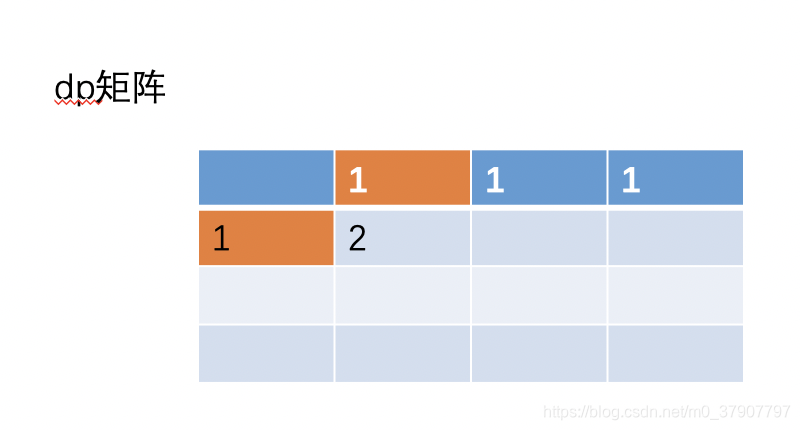
大家看图,以往的二维的时候, dp[i][j] = dp[i-1] [j]+ dp[i][j-1]。现在转化成一维,不就是 dp[i] = dp[i] + dp[i-1] 吗?
即 dp[1] = dp[1] + dp[0],而且还动态帮我们更新了 dp[1] 的值。因为刚开始 dp[i] 的保存第一行的值的,现在更新为保存第二行的值。

(3)、同样的道理,按照这样的模式一直来计算第二行的值,顺便把第一行的值抛弃掉,结果如下
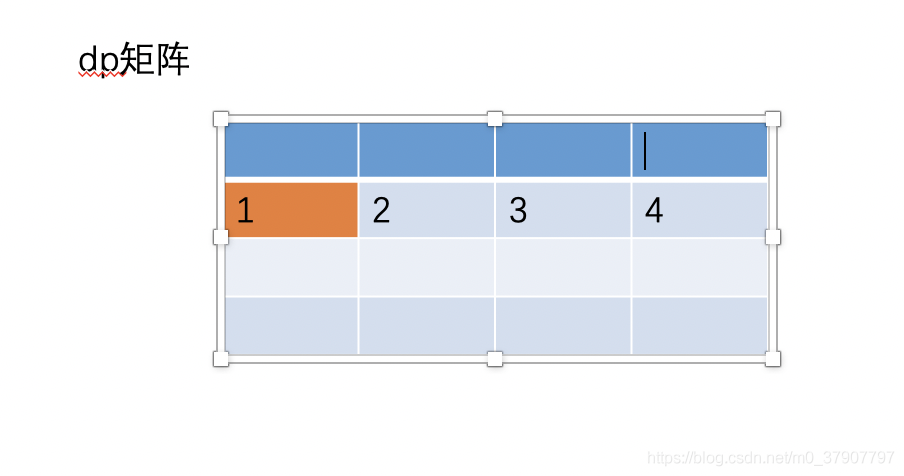
此时,dp[i] 将完全保存着第二行的值,并且我们可以推导出公式
dp[i] = dp[i-1] + dp[i]
dp[i-1] 相当于之前的 dp[i-1][j],dp[i] 相当于之前的 dp[i][j-1]。

