已知:如上图,机器人位于 s1,行动为 u,行动获得的奖励与题目的默认设置相同。在 s2 中执行各动作的 Q 值为:u: -24,r: -13,d: -0.29、l: +40,γ取0.9。
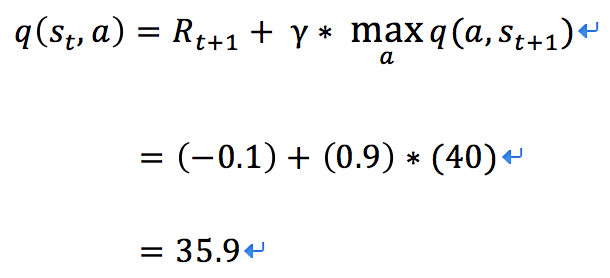
在强化学习中,「探索-利用」问题是非常重要的问题。具体来说,根据上面的定义,我们会尽可能地让机器人在每次选择最优的决策,来最大化长期奖励。但是这样做有如下的弊端:
在初步的学习中,我们的 Q 值会不准确,如果在这个时候都按照 Q 值来选择,那么会造成错误。
学习一段时间后,机器人的路线会相对固定,则机器人无法对环境进行有效的探索。
因此我们需要一种办法,来解决如上的问题,增加机器人的探索。由此我们考虑使用 epsilon-greedy 算法,即在小车选择动作的时候,以一部分的概率随机选择动作,以一部分的概率按照最优的 Q 值选择动作。同时,这个选择随机动作的概率应当随着训练的过程逐步减小。
在如下的代码块中,实现 epsilon-greedy 算法的逻辑,并运行测试代码。
import random import operator actions = ['u','r','d','l'] qline = {'u':1.2, 'r':-2.1, 'd':-24.5, 'l':27} epsilon = 0.3 # 以0.3的概率进行随机选择 def choose_action(epsilon): action = None if random.uniform(0,1.0) <= epsilon: # 以某一概率 action = random.choice(actions)# 实现对动作的随机选择 else: action = max(qline.items(), key=operator.itemgetter(1))[0] # 否则选择具有最大 Q 值的动作 return action

