Hello,大家好,我是bigsai,long time no see!在刷题和面试过程中,我们经常遇到一些排列组合类的问题,而全排列、组合、子集等问题更是非常经典问题。本篇文章就带你彻底搞懂全排列!
求全排列?
全排列即:n个元素取n个元素(所有元素)的所有排列组合情况。
求组合?
组合即:n个元素取m个元素的所有组合情况(非排列)。
求子集?
子集即:n个元素的所有子集(所有可能的组合情况)。
总的来说全排列数值个数是所有元素,不同的是排列顺序;而组合是选取固定个数的组合情况(不看排列);子集是对组合拓展,所有可能的组合情况(同不考虑排列)。
当然,这三种问题,有相似之处又略有所不同,我们接触到的全排列可能更多,所以你可以把组合和子集问题认为是全排列的拓展变形。且问题可能会遇到待处理字符是否有重复的情况。采取不同的策略去去重也是相当关键和重要的!在各个问题的具体求解上方法可能不少,在全排列上最流行的就是邻里互换法和回溯法,而其他的组合和子集问题是经典回溯问题。而本篇最重要和基础的就是要掌握这两种方法实现的无重复全排列,其他的都是基于这个进行变换和拓展。
全排列问题全排列,元素总数为最大,不同是排列的顺序。
无重复序列的全排列这个问题刚好在力扣46题是原题的,大家学完可以去a试试。
问题描述:
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]回溯法实现无重复全排列
回溯算法用来解决搜索问题,而全排列刚好也是一种搜索问题,先回顾一下什么是回溯算法:
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径.
而全排列刚好可以使用试探的方法去枚举所有中可能性。一个长度为n的序列或者集合。它的所有排列组合的可能性共有n!种。具体的试探策略如下:
从待选集合中选取第一个元素(共有n种情况),并标记该元素已经被使用不能再使用。
在步骤1的基础上进行递归到下一层,从剩余n-1个元素中按照1的方法找到一个元素并标记,继续向下递归。
当所有元素被标记后,顺序收集被标记的元素存储到结果中,当前层递归结束,回到上一层(同时将当前层标记的元素清除标记)。这样一直执行到最后。
回溯的流程如果从伪代码流程大致为这样:
递归函数: 如果集合所有元素被标记: 将临时储存添加到结果集中 否则: 从集合中未标记的元素中选取一个存储到临时集合中 标记该元素被使用 下一层递归函数 (这层递归结束)标记该元素未被使用如果用序列 1 2 3 4来表示这么回溯的一个过程,可以用这张图来显示:
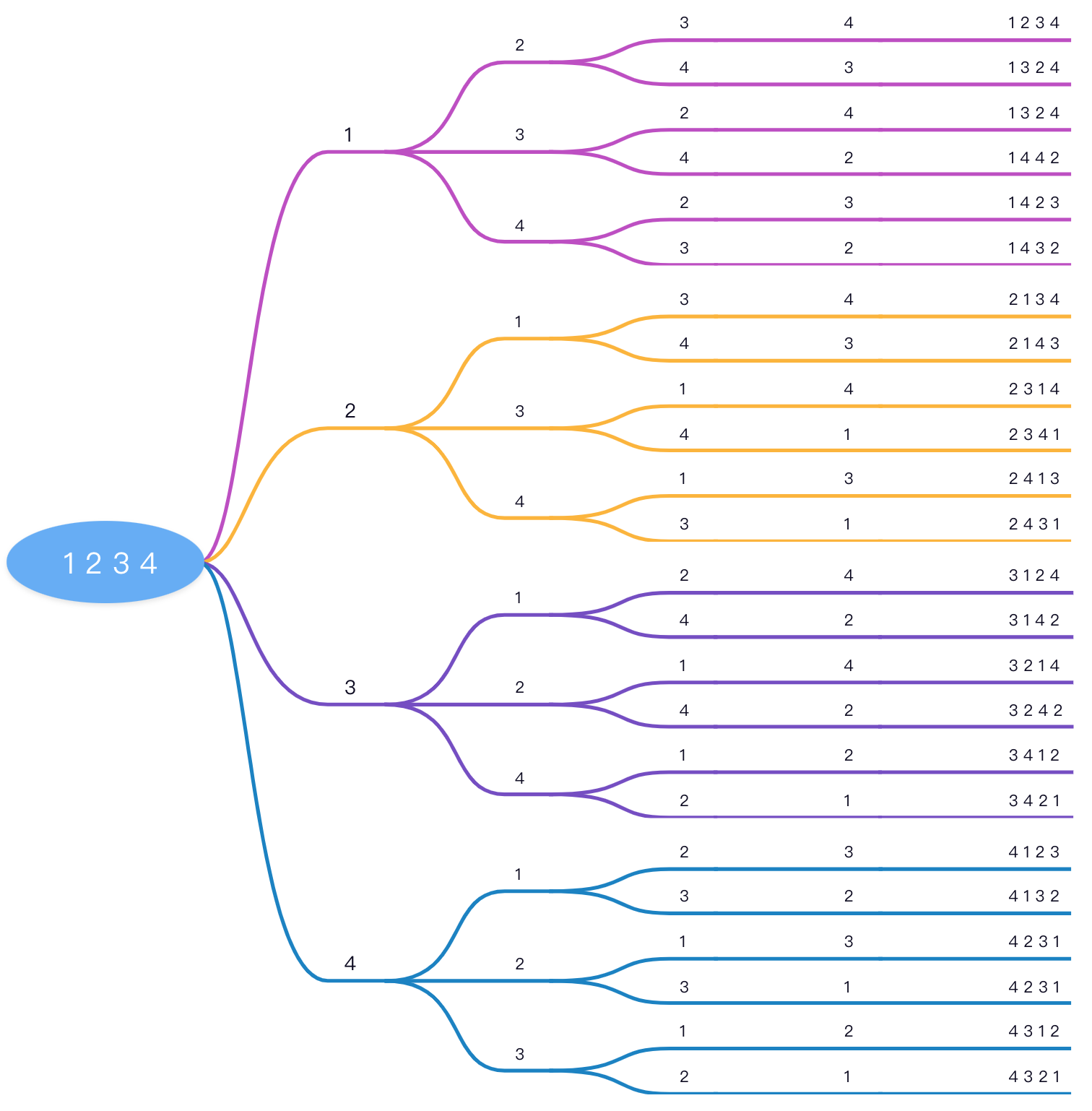
用代码来实现思路也是比较多的,需要一个List去存储临时结果是很有必要的,但是对于原集合我们标记也有两种处理思路,第一种是使用List存储集合,使用过就移除然后递归下一层,递归完毕后再添加到原来位置。另一种思路就是使用固定数组存储,使用过对应位置使用一个boolean数组对应位置标记一下,递归结束后再还原。因为List频繁查找插入删除效率一般比较低,所以我们一般使用一个boolean数组去标记该位置元素是否被使用。
具体实现的代码为:
List<List<Integer>> list; public List<List<Integer>> permuteUnique(int[] nums) { list=new ArrayList<List<Integer>>();//最终的结果 List<Integer> team=new ArrayList<Integer>();//回溯过程收集元素 boolean jud[]=new boolean[nums.length];//用来标记 dfs(jud, nums, team, 0); return list; } private void dfs(boolean[] jud, int[] nums, List<Integer> team, int index) { int len = nums.length; if (index == len)// 停止 { list.add(new ArrayList<Integer>(team)); } else for (int i = 0; i < len; i++) { if (jud[i]) //当前数字被用过 当前即不可用 continue; team.add(nums[i]); jud[i]=true;//标记该元素被使用 dfs(jud, nums, team, index + 1); jud[i] = false;// 还原 team.remove(index);//将结果移除临时集合 } }修改一下输出的结果和上面思维导图也是一致的:

邻里互换法实现无重复全排列

